102

102

7. Wektory losowe

Dla dwuwymiarowego przypadku dyskretnego niezależność zmiennych losowych X i Y jest równoważna relacji

Pij = P jPi-.    (⁷-2.2)

która musi być spełniona dla dowolnej pary (x_jty ■).

k/

Jeśli (X,Y) będzie wektorem typu ciągłego o gęstości f(x,y), to gęstość zmiennej losowej X oznaczymy przez f_x(x), a zmiennej losowej Y oznaczymy przez f_Y(y)- Wtedy

fx W = V f(^x>y)^dy ■

Analogiczny związek zachodzi dla zmiennej losowej Y.

Rozpatrzmy teraz dwa przykłady rozkładów - rozkładu dyskretnego, oraz rozkładu typu ciągłego.

Dwuwymiarowy rozkład dyskretny

Przykład. Rzucamy dwiema kostkami do gry. Niech X będzie liczbą oczek na pierwszej kostce, Z na drugiej, a Y większym z tych wyników, czyli Y = max{X,Z} Otrzymujemy w ten sposób dyskretny wektor losowy (X,7). Jego rozkład, czyli prawdopodobieństwa /?■<, można przedstawić w postaci

ł/

macierzy

~ 1/36	1/36	1/36	1/36	1/36	1/36 '
0	2/36	1/36	1/36	1/36	1/36
0	0	3/36	1/36	1/36	1/36
0	0	0	4/36	1/36	1/36
0	0	0	0	5/36	1/36
0	0	0	0	0	6/36 _

Sposób otrzymania tej macierzy objaśnimy na przykładzie. Wynik (2,4) otrzymamy wtedy, gdy na pierwszej kostce wypadną dwa oczka, a na drugiej cztery. Prawdopodobieństwo tego wynosi (1/6) (1/6)= 1/36. Wynik (4,2) jest niemożliwy, a wynik (2,2) otrzymamy wtedy, gdy na pierwszej kostce będą dwa oczka, a na drugiej jedno lub dwa oczka. Prawdopodobieństwo tego wynosi (1 /6) (2/6) = 2/36. Korzystając ze wzoru (7.2.1) otrzymujemy, że Pi. — 1/6, (co jest oczywiste, bo X jest liczbą oczek na pierwszej kostce) oraz P.j ~ (2/ — l)/36. Widać, że relacja (7.2.2) nie jest spełniona, więc zmienne losowe X i Y nie są niezależne.

Dwuwymiarowy rozkład typu ciągłego

Przykład. Niech T będzie trójkątem ograniczonym osiami układu współrzędnych i prostą o równaniu y — 1 — x. Niech

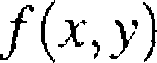
2 dla (x,y) € 7\ 0 dla (x,y) </ T

(7.2.3)