096

7. Wektory losowe
7.1. Rozkłady dwuwymiarowe
Przykłady
Przykład 7.1.1.
Niech
,, X fc^+y2) dla (x,y) € K,
f(xiy) = i n
^0 poza tym,
gdzie K = {(x,y) € R2 : 0 ^ x < l,x — 1 < y < 1 —x}.
a) Wyznaczyć stałą c tak, aby funkcja f(x,y) była gęstością pewnej zmiennej losowej
(X,Y).
b) Obliczyć Pr(X2 + Y2 ^ 0.5).
Rozwiązanie.
a) Stałą c wyznacza się z równania
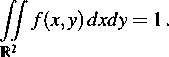
Stąd
1 l-x

a więc c = 3.
Wyszukiwarka
Podobne podstrony:
97 7.1. Rozkłady dwuwymiarowe b) Pr(X2 + Y2 < .0.5) = jj f(x,y)dxdy, gdzie A = {(x,y) (= K : x2 +
7. Wektory losowe7.1. Rozkłady wielowymiarowe7.1.1. Dystrybuanty Do tej pory rozważając ciąg zmienny
S6300963 przykra0* d) Niech ponadto , / _ i oraz x ń ---dla n € N. Wtedy mamy lim
Rozkłady dwuwymiarowe, niezależność zmiennych 1 .Wektor losowy (X,Y). Niech rozkład wektora losowego
100 Niezależne zmienne losowe Typy rozkładów 7. Wektory losowe Odpowiednikiem wariancji dla
102 7. Wektory losowe dla x € [0,1]. Dla x <G (0,1 /2): .V 1 m2(x) = I 2ydy+ j
102 7. Wektory losowe Dla dwuwymiarowego przypadku dyskretnego niezależność zmiennych losowych X i Y
108 7. Wektory losowe Dwuwymiarowy rozkład normalny7.3.2. Wielowymiarowy rozkład normalny Zdefiniuje
więcej podobnych podstron