3544073511

Rozkłady dwuwymiarowe, niezależność zmiennych

1 .Wektor losowy (X,Y). Niech rozkład wektora losowego (X,Y) wyraża się macierzą P gdzie oznacza prawdopodobieństwo przyjęcia przez wektor X

wartości    gdzie y_x = O,y₂= \,y₃ = 2 zaś *1 ⁼ 0,x_y = 1 , P-

I I o

4 3

O i I

4 ój

Znajdź dystrybuantę wektora losowego, zbadaj niezależność zmiennych X, Y.

2. Rzucamy 2 razy kostką do gry. Niech X liczba oczek w pierwszym rzucie, a

Y    suma liczby oczek w obu rzutach Zbadaj rozkład wektora (X, Y). Znajdź rozkłady brzegowe. Zbadaj niezależność zmiennych X i Y.

3.    Rzucamy 2 razy kostką do gry. Niech X liczba oczek w pierwszym rzucie, a

Y    suma liczby oczek w obu rzutach Zbadaj rozkład wektora (X, Y). Znajdź rozkłady brzegowe. Zbadaj niezależność zmiennych X i Y.

4. Rzucamy 2 razy kostką do gry. Niech X minimum wyników z obu rzutów, a

Y    maksimum wyników z obu rzutów. Zbadaj rozkład wektora (X, Y). Znajdź rozkłady brzegowe. Zbadaj niezależność zmiennych X i Y.

5. Dobierz stałą c tak aby funkcja: f_xx(^x,y) =

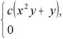
dla xe [0,l] i ye [o,2] dla pozostaych x, y

była gęstością dwuwymiarową wektora (X, Y). Znajdź rozkłady brzegowe. Zbadaj niezależność zmiennych X i Y. Znajdź dystrybuantę dwuwymiarową.

, v \ce~^{xty\ dla x>0iy>9

6. Dobierz stałą c tak aby funkcja: f_{x r}\x,y) = \    była

^{1 A}    dla pozostaych x,y

gęstością dwuwymiarową wektora (X, Y). Znajdź rozkłady brzegowe. Zbadaj niezależność zmiennych X i Y. Znajdź dystrybuantę dwuwymiarową.

cy, dla 0< x< —iyz [0,l]

y    była

O dla pozostaych x,y

7. Dobierz stałą c tak aby funkcja: f_xx{^x,y) =

gęstością dwuwymiarową wektora (X, Y). Znajdź rozkłady brzegowe. Zbadaj niezależność zmiennych X i Y. Znajdź dystrybuantę dwuwymiarową.

8. Znajdź macierz kowariancji dla wektorów losowych z zadań 1,2,3,4,5,6.

9.Niech funkcja: f_xxi^x,y) =

2’

dla (x,_y)e D

gdzie

O dla pozostaych x,y

D = {(x,_y) e R² : |y- x| < 1 / x| < l}, gęstość dwuwymiarowego wektora (X, Y). Zbadaj niezależność zmiennych X i Y. Policz, że E(XY)=E(X)-E(Y).

13