97899
Rozkład dwumianowy BernouUi'ego B(n, p)
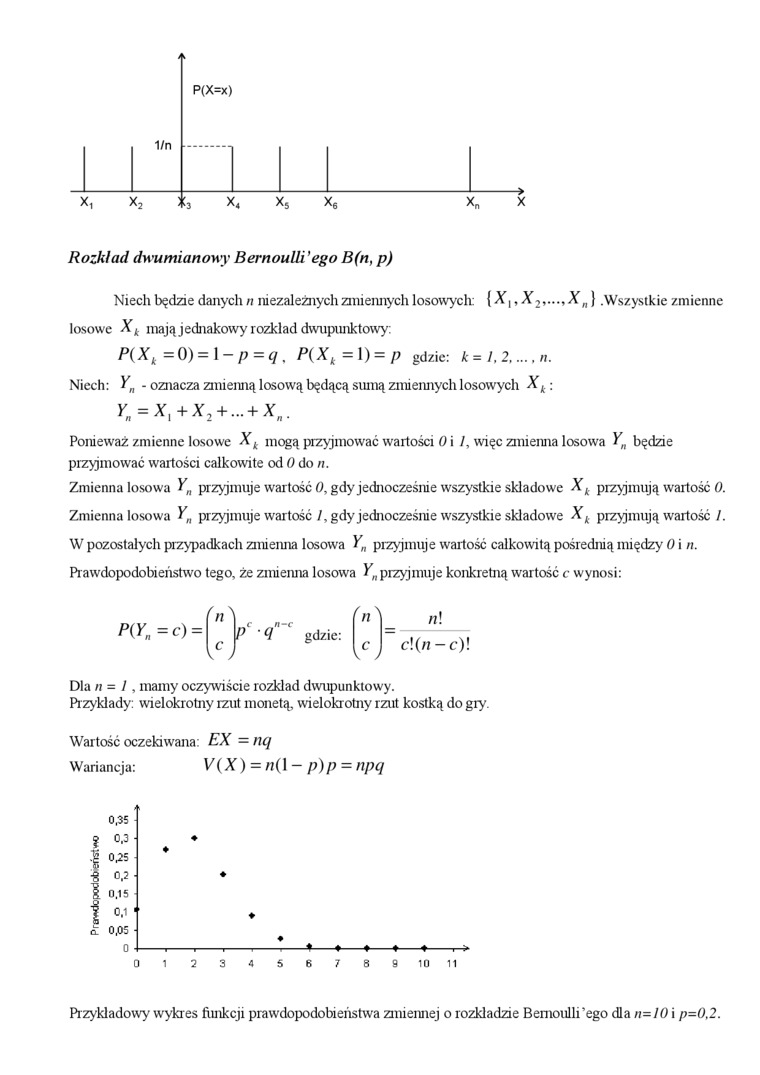
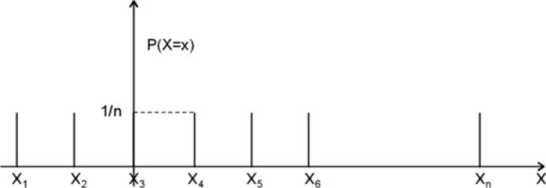
Niech będzie danych n niezależnych zmiennych losowych: {, X2,...t X n) .Wszystkie zmienne losowe Xk mają jednakowy rozkład dwupnnktowy:
P(X, =0)=\-p=q , P(Xk=\) = p gdzie: k= 1,2.....n.
Niech: - oznacza zmienną losową będącą sumą zmiennych losowych X k:
Ym = Xl+Xt + ... + Xm.
Ponieważ zmienne losowe Xk mogą przyjmować wartości 0 i /, więc zmienna losowa Yn będzie przyjmować wartości całkowite od 0 do n.
Zmienna losowa Yn przyjmuje wartość 0, gdy jednocześnie wszystkie składowe Xk przyjmują wartość 0. Zmienna losowa Yn przyjmuje wartość /, gdy jednocześnie wszystkie składowe Xk przyjmują wartość /. W pozostałych przypadkach zmienna losowa Yn przyjmuje wartość całkowitą pośrednią między 0 i n. Prawdopodobieństwo tego, że zmienna losowa Yn przyjmuje konkretną wartość c wynosi:
|
f") |
c |
n-c | |
|
* |
p q |
gdzie: |
<C j |
Dla n = 1, mamy oczywiście rozkład dwupunktowy.
Pr zyklady: wielokrotny rzut monetą, wielokrotny rzut kostką do gry.
Wartość oczekiwana: EX = nq
Wariancja: V( X) = n{ 1 - p) p = npą
0,35 % 0.3
I ^
•8 0.2
1 0.15
1 0,1
Cl 0,05
o
Przykładowy wykres funkcji prawdopodobieństwa zmiennej o rozkładzie Bemoulli’ego dla n-10 i p=0,2.
Wyszukiwarka
Podobne podstrony:
CCF20101004�017 M i 7. Rozkład dwumianowy (Bernoulliego) i rozkład Poissona liczby zliczeń (h ■= P T
56 2. Zmienne losowe 2.4.9*. Niech X i S będą niezależnymi zmiennymi losowymi takimi, że X będzie mi
56 2. Zmienne losowe 2.4.9*. Niech X i S będą niezależnymi zmiennymi losowymi takimi, że X będzie mi
33,34 Rozkład normalny (gaussowski) Def. Niech X będzie zmienną losową o gęstości prawdopodobieństwa
52048 Str081 158 5. I .terby pierwsze i rozkład na czynniki Twierdzenie 5.1.1. Nie
img108 10?:Ekstrema warunkowe Niech f będzie funkcję rzeczywisty n zmiennych rzeczywistych x.,...,xn
CZESC< (2) 3. Niech dane będą niezależne zmienne losowe X, Y takie, ze X ~ A^/w^cr,), Y ~ iV(77i2,cr
70 i. Twierdzenia graniczne 3.2.2. Niezależne zmienne losowe X, ,X2,... ,X60 mają rozkład jednostajn
73 5.1. Estymacja punktowaZadaniaZadanie 5.1.1. Niech Xy,X2,X3 będą niezależnymi zmiennymi losowymi
74 5. EstymacjaZadanie 5.1.6*. Niech Xl,X2,...,Xn będą niezależnymi zmiennymi losowymi o jednakowych
33 2.1. Rozkłady i parametry zmiennych losowychZadanie 2.1.8. Niezależne zmienne losowe X, i X2 mają
2. Zmienne losowe 19 2.4. Estymatory 155. Niech X,..., Xn będą niezależnymi zmienn
więcej podobnych podstron