074

74

5. Estymacja

Zadanie 5.1.6*.

Niech X_l,X₂,...,X_n będą niezależnymi zmiennymi losowymi o jednakowych rozkładach normalnych N(m, a). Dla jakiej wartości k estymator

V = k'£\X_j-X\ j=i

jest nieobciążonym estymatorem parametru <7?

Zadanie 5.1.7.

Poniższe dane pochodzą z rozkładu normalnego N(0.35,2.1), (plik normal35. dta). -1.09, -1.44,    1.46, -0.48, 3.03, 1.71, -1.23, -0.28, -4.96, 0.44,

3.68, -0.92, -2.23, -2.23, 1.98, 1.23, 0.61,    1.79, -1.96, -1.73.

Obliczyć x oraz oszacować parametr a² korzystając z estymatorów:

a)    S²,

b)    S²,

c)    W² z zadania 5.1.5.

d)    V z zadania 5.1.6 z wyznaczonym k,

Porównać oszacowania z prawdziwymi wartościami m i a².

Zadanie 5.1.8.

Niech X_vX₂,...,X_n będzie próbą prostą z rozkładu jednostajnego na odcinku [0,0], Niech Z„ = max{.Xj ,X₂, ■ ■ ■ ,X_n}. a) Uzasadnić, że dystrybuanta statystyki Z„ wyraża się wzorem

fo

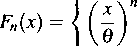
1

V

dla x < 0, dla 0 < x < 0, dla x> 9.

b)    Wyznaczyć gęstość zmiennej losowej Z„.

c)    Wykazać, że estymator

T_n =

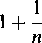
Zn

jest estymatorem nieobciążonym i zgodnym parametru 0.

Zadanie 5.1.9*.

Niech X_l,...,X_n będzie próbą prostą z populacji o rozkładzie jednostajnym na odcinku [0,a]. Niech

n +1    .    .    2 ^

T\ —-maxX_lr..,I„, r₂ = -^X,.

n    n rr'

i=i

będą estymatorami parametru a. Wykazać, że oba estymatory są nieobciążone oraz że estymator 7, jest lepszy od T₂.