056

56

2. Zmienne losowe

2.4.9*. Niech X i S będą niezależnymi zmiennymi losowymi takimi, że X będzie miała rozkład wykładniczy oraz Pr(S = 1) — Pr(S = -1) — 1/2. Znaleźć rozkład zmiennej losowej Z — SX.

2.4.10.    Niech Y — aX + b, a > 0 oraz niech X ma dystrybuantę F(x) i gęstość f(x). Znaleźć dystrybuantę i gęstość zmiennej losowej Y.

2.4.11.    Niech zmienna losowa X ma rozkład normalny N(0,1). Obliczyć D²X.

2.4.12*. Niech zmienna losowa X ma rozkład normalny N(0,1). Obliczyć EX³ i EX⁴. Niech Y - X². Obliczyć D²F.

p

2.4.13 . Korzystając z rozwinięcia gęstości rozkładu normalnego w szereg Maclaurina, znaleźć rozwinięcie dystrybuanty. Korzystając z tego rozwinięcia napisać procedurę obliczania wartości dystrybuanty 4> rozkładu normalnego N(m, ct).

Rozkład Pareto 2.4.14. Rozkładem Pareto¹⁰ nazywa się rozkład (stosowany często w ekonomii) o gęstości

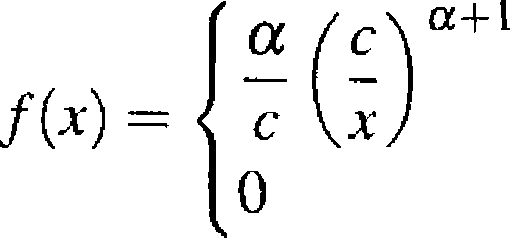
dla x > c, dla x ^ c,

gdzie c > 0 i a > 0. Dla jakich a istnieją momenty rzędu kl Obliczyć te momenty oraz wariancję.

2.4.15.    Korzystając z tablic wartości krytycznych rozkładu chi-kwadrat, znaleźć Xa takie, że Pr (%² > xV) ^{= a} oraz Pr (z² < Za) — 1 — cc dla a — 0.1, a — 0.05 i a = 0.01, gdy zmienna losowa x² rna rozkład chi-kwadrat on = 2, n — 5 i n = 15 stopniach swobody.

2.4.16.    Korzystając z tablic wartości krytycznych rozkładu f-Studenta, znaleźć t_a takie, że Pr (t > t_a) = a oraz Pr (t < t_a) = 1 — a dla a = 0.1, a — 0.05 i a = 0.01, gdy zmienna losowa t ma rozkład f-Studenta on = 2,n = 5 \ n = \5 stopniach swobody.

2.4.17.    Korzystając z tablic wartości krytycznych rozkładu chi-kwadrat, znaleźć Pr(x² < ■*) dla zmiennej losowej o rozkładzie chi-kwadrat on = 2,n~5 i n — 15 stopniach swobody oraz x = 0.5 i x = 5.

2.4.18.    Korzystając z tablic wartości krytycznych rozkładu Snedecora, znaleźć F_a takie, że Pr(F > F_a) = a dla a = 0.05 i a = 0.95, gdy zmienna losowa F ma rozkład Snedecora o (3,11) i (11,3) stopniach swobody.

^t0Vilfredo Pareto (1848 - 1923), włoski socjolog i ekonomista.