070

70

i. Twierdzenia graniczne

3.2.2. Niezależne zmienne losowe X, ,X₂,... ,X₆₀ mają rozkład jednostajny na odcinku [1,3]. Niech

60

* = £**

k= 1

Obliczyć przybliżoną wartość wyrażeń Pr(X > 130), Pr(X < 115) oraz Pr(118 < X < 123). Które z tych przybliżeń można otrzymać z nierówności Markowa lub Czebyszewa? Porównać dokładność tych oszacowań.

3.2.3. Niezależne zmienne losowe X_{ ,X₂,... ,X₁₀₀ mają rozkład Poissona o parametrze A =2.5. Obliczyć przybliżoną wartość wyrażenia

too

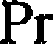
J2x_k> 220

k= 1

3.2.4. Znaleźć %a takie, że Pr {%² > Xa) = oc dla a = 0.1, a = 0.05 i a = 0.01, gdy zmienna losowa %² ma rozkład chi-kwadrat Pearsona o n = 35, n = 60 i n = 150 stopniach swobody.

3.2.5. Wykonać to samo co w zadaniu 3.2.4, ale dla zmiennej losowej t = 11 gdy t ma rozkład f-Studenta.

3.2.6. Znaleźć Pr(#² < x) dla zmiennej losowej o rozkładzie chi-kwadrat Pearsona o n — 35, n = 60 i n = 150 stopniach swobody oraz a =-- 0.5 i jc = 5.

3.2.7. Wykonać to samo co w zadaniu 3.2.6, ale dla zmiennej losowej f, o rozkładzie r-Studenta.

3.2.8. Niech niezależne zmienne losowe X_k mają rozkłady jednostajne na odcinkach (-&,£), czyli gęstość zmiennych losowych X_k jest postaci

gdzie k~ 1,2,.... Sprawdzić, czy są spełnione założenia twierdzenia Lapu-nowa.