103

103

7.2. Rozkłady dwuwymiarowe

będzie gęstością wektora (X, Y). Gęstości brzegowe tego wektora mają postać:

°°    1—X

fxM = Jf(^x,y)^d>’= j 2dy = 2(1 -x).

-oo    0

dla jc € [0,1]. Dla jc ^ [0,1] mamy f_x(x) = 0. Przez symetrię otrzymujemy wzór f_Y(y) = 2(1 -y) dla y e [0,1] oraz f_Y(y) = 0 dla y [0,1]. Z tego wynika, że f(x,y) 7^ fx(^x)fy(y)' Zatem zmienne losowe X i Y nie są niezależne.

7.2.2. Rozkłady warunkowe

Określimy teraz rozkłady warunkowe dla dwuwymiarowych wektorów losowych (X,F). Dla uproszczenia uczynimy to osobno dla rozkładów dyskretnych, a osobno dla rozkładów typu ciągłego.

Definicja.

Rozkład warunkowy dyskretnej zmiennej losowej X względem dyskretnej zmiennej losowej Y określamy wzorem

Pi\J =

_ PiJ

P.

(7.2.4)

j

Gęstość

warunkowa

a dla rozkładu typu ciągłego rozkład warunkowy zmiennej losowej X względem zmiennej losowej Y określamy przez podanie funkcji zwanej gęstością warunkową. Jest ona określona wzorem

My) =

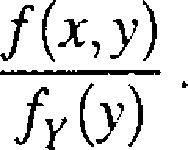
(7.2.5)

Dystrybuanta

warunkowa

Mlmtów

)tykrOtnych

Dystrybuanta warunkowa rozkładów typu ciągłego

Zauważmy, że przy ustalonym j (dla rozkładu dyskretnego) lub ustalonym y (dla rozkładu typu ciągłego) wzory (7.2.4) i (7.2.5) dają nam poprawnie określone rozkłady zmiennych losowych X. Jeśli oznaczymy przez F(*|y) dystrybuantę takiego rozkładu warunkowego, zwaną dystrybuantą warunkową,

* i * .    € * . t...... t * f ? ----i_______: v    £

traktować jalcG    zmiennei losowej V \

r{x\y) = Pr(X < x\Y = y).

Trzeba jednak zwrócić uwagę, że wzór ten jest w pełni poprawny tylko dla zmiennych losowych dyskretnych, natomiast dla innych rozkładów w warun-

ku może pojawić się zdarzenie {Y =y} o prawdopodobieństwie zerowym.

Jednakże dla zmiennych losowych typu ciągłego dystrybuanta warunkowa zmiennej losowej X przy warunku Y = y jest określona zależnością

X

^F(x\y)= j f(t\y)dt,    (7.2.6)

— oo

zgodnie ze wzorem (2.1.3). Zwróćmy tu uwagę, że bezpośrednio z definicji wynika, że dla niezależnych zmiennych losowych X i Y mamy F(x\y) = F_x(x).