109

109

7.2. Parametry rozkładów dwuwymiarowych

gdzie x_t, yj są środkami odpowiednich klas, a liczbami wyników takich, że cecha X należy do klasy r-tej, a cecha Y do klasy 7 - tej. Stąd r = —0.4818. Przedział ufności wyznaczamy ze wzoru

Pr

1 — r²

r + u_a

= 1 - a,

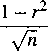
gdzie Pr(|t/| < u_a) = 1 — a dla U ~ N(0,1). Stąd u_a = 1.96 i ostatecznie p G (-0.55,-0.41).

Zadania

Zadanie 7.2.1.

Dwie niezależne zmienne losowe X i Y mają rozkłady normalne N(m,a) z takimi samymi parametrami. Znaleźć współczynnik korelacji zmiennych losowych U = aX +bY i V = aX-bY.

Zadanie 7.2.2.

Zmienna losowa (X,P) ma rozkład prawdopodobieństwa podany w tabeli:

	2	4
-i	0.1	0.06
0	0.3	0.18
i	0.2	0.16

Obliczyć współczynnik korelacji.

Zadanie 7.2.3.

Zmienna losowa dwuwymiarowa (X,Y) ma rozkład podany w tabelce:

\^A>	1	2	3	4	5
1	2/24	4/24	0	3/24	3/24
2	2/24	1/24	2/24	1/24	0
3	2/24	1/24	0	1/24	2/24

Obliczyć współczynnik korelacji X i Y.

Zadanie 7.2.4.

Wektor losowy (X,Y) ma gęstość wyrażającą się wzorem

f(x,y)

A dla (x,y) e V, 0 dla (x,y) ^ V,

gdzie V jest obszarem ograniczonym półokręgiem o promieniu 1, położonym nad osią Ox. Obliczyć E(Xy).