109

109

13. Parametry rozkładów dwuwymiarowych

z twierdzenia 7.3.4. Zgodnie z tym twierdzeniem normalne są X N(3, \/2) i Y ~ N(0, v3), wystarczy więc obliczyć jeszcze tylko Cov(X, Y). Zgodnie ze

wzorem (7.3.2) musimy obliczyć

E(XY) = E((Z₁ + Z₂)(2Z_l - Z₂)) = 2EZi - EZf + EZ_tZ₂ .

Ponieważ dla dowolnej zmiennej losowej Z, mamy EZf = D²Z_i + (EZ_y)², więc E(X7) = 2(1 + 1)—4+1 = 1, skąd Cov(X,7) = 1. Stąd i ze wzoru (7.3.3) otrzymujemy p = l/\/£. Zauważmy na koniec, że dla obliczenia współczynnika korelacji nie było potrzebne założenie o normalności Z_{ i Z₂, a tylko założenie o niezależności. Założenie o normalności jest natomiast niezbędne dla normalności wektora (X,7).

Rozkład

normalny

n-wymiarowy

Na koniec podamy gęstość rozkładu normalnego n-wymiarowego o macierzy kowariancji symetrycznej i dodatnio określonej oraz o wektorze wartości oczekiwanych m — (m_t,... ,m_rt). Wyraża się ona wzorem:

(x-m)R ^l(x-m)^TJ ,    (7.3.7)

^aS^expH

gdzie x — (jcj, ... ,x_n).

7.3.3. Estymacja i testowanie współczynnika korelacji

Niech ((ZpZj),..., (X„,7_n)) będzie n-ełementową próbą prostą. Chcemy znaleźć estymator współczynnika korelacji p(X,Y). Statystyka określona wzorem

Estymator

współczynnika

korelacji

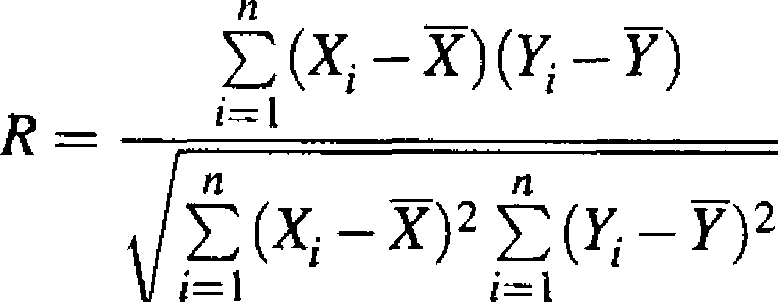
(7.3.8)

jest estymatorem zgodnym współczynnika korelacji p.

Jeśli próba jest liczna, to wygodnie jest podzielić dane na klasy w tablicę wie-Iodziełczą, opisaną w punkcie 6.2.2. Wtedy, jeśli wartości cechy X podzielimy na k klas, a wartości cechy Y na / klas, to estymator dany wzorem (7.3.8) przybierze postać:

(7.3.9)

gdzie +, y ■ są środkami odpowiednich klas.