111

111

7.3. Parametry rozkładów dwuwymiarowych

czyli w zaokrągleniu (0.07,0.17). Jeżeli dla tych samych danych będziemy testować hipotezę H_Q : p = 0 (tzn. w tym przypadku hipotezę o niezależności X i 7), przeciw hipotezie H_x : p > 0, to trzeba ze wzoru (7.3.11) obliczyć t. Ze względu na duże n rozkład tej statystyki jest prawie normalny, a więc u_a = 1.65, gdyż dla U ~ N(0,1) mamy Pr(£7 < 3.65) ^ 0.95. Po podstawieniu do wzoru otrzymujemy

t =

0.12

70.9856

7398 « 2.41,

a więc hipotezę o niezależności należy odrzucić na korzyść hipotezy, że p > 0. Postawmy teraz hipotezę, że p = 0.1 przeciwko hipotezie p ^ 0.3. Skorzystamy teraz ze statystyki określonej wzorem (7.3.12). Mamy tu

u

= ^1.1513 w 0.4009.

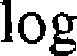
1+0.12

1-0.32

1+0.1 1 -0.3

0.1

2+599

\/397

Ponieważ u ~ 0.4009 < 1.96 — w_a, więc nie ma podstaw do odrzucenia hipotezy, że p — 0.1.

7.3.4. Proste regresji

Sformułujmy teraz problem minimalizacji, jak we wzorze (7.2.8), ale ograniczając się wyłącznie do funkcji postaci f(x) — ax + j3. Mówimy wtedy o regresji drugiego rodzaju. Dokładniej, będziemy poszukiwać współczynników

a i P takich, aby wyrażenie E ^(Y — (aX + j3))²j było najmniejsze, czyli

będziemy poszukiwać najlepszego przybliżenia zmiennej losowej Y liniową funkcją zmiennej losowej X.

Twierdzenie 7.3.7.

Wyrażenie E ^(P — (aX + j3))²^ osiąga najmniejszą wartość, tylko gdy współczynniki regresji a i p są określone wzorami

a = p—, P=m_0l-p

m

a

i

a

10’

i

legresja 'rugiego odzaju

gdzie af — D^ZX, cĄ — D²P, m_xo = EX oraz m_QX = EY Prostą o równaniu

>’-^mot

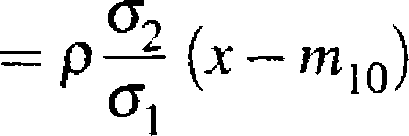
nazywa się prostą regresji lub regresją drugiego rodzaju.