133

133

s.

Analizę wariancji dla modelu klasyfikacji pojedynczej można przedstawić w formie tablicy (tablica 6.4).

Tablica 6.4

Analiza wariaricyjna. Klasyfikacja pojedyncza

Zmienność	Liczba stopni swobody K	Suma kwadratów odchyleń n S^2	Średni kwadrat V	F°	F
Między obiektami MO	^Kob = ^C“^1	^tóob = Z (?!-?)^2	nS^2h v ^ob ^Vob ^	„o ^Vob t =~y~ e
Wewnątrz obiektów WO '•	Ke = n-e	^nSe ^= 2 ^(yij^-yj^^2	^nse ^Ve “ e
Całkowita C	Ky = n-1	^nSy “ Z(^yij"^y)^2		i

6.3. fRZEDSTAWIANIE DANYCH W POSTACI ZALEŻNOŚCI MATEMATYCZNYCH

(

6.3.1. Współczynnik korelacji prostoliniowej

\

Marą ilościową związku pomiędzy zmiennymi jest współczynnik korelacji. Współczynnik korelacji wynoszący jeden (r = 1), oznacza całkowite powiązanie zmiennych. Natomiast całkowicie przypadkowy związek występuje, gdy wartość współczynnika korelacji wynosi zero.

Stawiając hipotezę, że nie ma żadnego związku między zmiennymi x i y dla korelacji prostoliniowej, współczynnik korelacji możemy wyrazić w postaci:

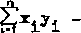
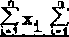
^yi

n

172

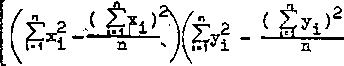
(6.25)

gdzie: n - liczba danych.

fil

Obliczoną wartość współczynnika r z zależności (6.25) sprawdzamy z wartościami współczynnika korelacji podanymi w tablicy 6,5 na danym po—