083

5.1. Estymacja punktowa

83

Przykład. Dla rozkładu wykładniczego (określonego wzorem (2.4.1)) z parametrem A mamy

L(A) = Aⁿe

— A (x j +A^_2 H-----ł-X_;!)

Po zlogarytmowaniu i zróżniczkowaniu otrzymujemy równanie

n    .

~ — (Xi + A*2 -)-----h x_n) — 0,

a więc A — 1 /X.

Jeśli L nie jest różniczkował-na

Jeżeli L nie jest funkcją różniczkowalną, to jej maksimum nie może być znalezione w ten sposób.

Przykład. Niech X ma rozkład jednostajny na odcinku [0,a]. Wtedy

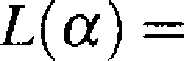
1 jaⁿ dla max{.vj < a, 0 dla a < maKl^}.

Taka funkcja L osiąga maksimum w punkcie a — max{xj, w którym nie ma pochodnej. Stąd a — max{X_/}. Jeśli X ma rozkład jednostajny na [a,/?], to a — min{Xj, b = max{X_J}.

5.1.4. Zadania

5.1.1.    Niech X_x ,X₂,.. .X_n będą niezależnymi zmiennymi losowymi o jednakowych rozkładach normalnych N(m,a). Dobrać stałą k tak, aby funkcja

w²=*E(x₊i-x)²

i—1

była nieobciążonym estymatorem wariancji.

5.1.2.    Skonstruować metodą momentów estymatory parametrów p i n rozkładu dwumianowego.

5.1.3.    Gęstość wyraża się wzorem

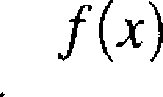
0    dla jc < a,

fi /x²    dla x a,

gdzie a > 0. Obliczyć fi i następnie metodą największej wiarogodności wy znaczyć estymator parametru a.