043

43

2.3. Rozkłady dyskretne

określoną wzorem (2.3.1) można interpretować jako liczbę sukcesów (jedy-nek) w ciągu niezależnych doświadczeń, zwanych próbami Bernoulliego, w których prawdopodobieństwo sukcesu (jedynki) jest równe p, a porażki (zera) jest równe q = 1 — p.

Przykład. Wykonujemy ciąg n = 10 prób Bernoulliego. W każdej z nich odnosimy sukces z prawdopodobieństwem p = 0.9. Jakie jest prawdopodobieństwo, że w dokładnie jednej próbie (tzn. w 10% wszystkich prób) odniesiemy sukces. W tym przypadku rozwiązanie jest proste:

Pr(X = l)= r⁰)0.9'0.1⁹ = 910“⁹.

Co jednak będzie, gdy przy tym samym n przyjmiemy p — 0.09? Obliczenie liczby 0.09 0.91⁹ jest już kłopotliwe, a obliczenie prawdopodobieństwa, że uda się nie więcej niż 10% doświadczeń z 1000 prób jest już praktycznie bardzo trudne. Spróbujmy bowiem bezpośrednio i dokładnie obliczyć

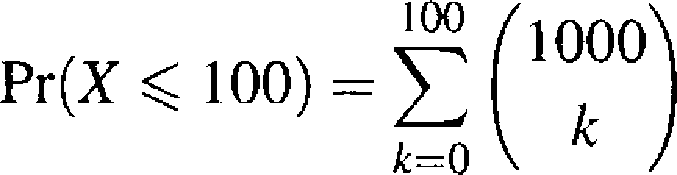
1000 /: p q

Napisanie procedur (np. w Pascalu lub C) wykorzystujących wprost wzory (2.3.2) i obliczających współczynniki Newtona ze wzoru rekurencyjnego

n

k

n — 1

k- 1

+

n — 1

nie daje zadowalających efektów dla większych n i k.

Wzór

rekurencyjny

Dla wygody przyjmiemy oznaczenie

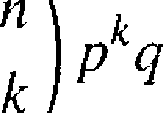
n—k

b(n,k,p)

Jest to prawdopodobieństwo otrzymania w n niezależnych próbach k sukcesów, gdy prawdopodobieństwo sukcesu w pojedynczej próbie jest równe p.

Łatwo jest teraz udowodnić wzór rekurencyjny

b(n,0,p) b(n,k+\,p)

(2.3.3)

n-kp ,    \

(2.3.4)

Wzór ten do bezpośredniego zaprogramowania nadaje się w równie małym stopniu jak i wzór (2.3.2), ale stanowić będzie podstawę dla efektywnych przybliżeń rozpatrywanych w następnym punkcie,