171
Rozwiązanie. Impedancje w postaci operatorowej obydwu gałęzi aą równe: Zj(») <=+*Ł» Z2{i) =“ Ri+-ję.
Prąd w gałęzi z kondensatorem określony jest zależnością Napięcie na kondensatorze określone jest wyrażaniem
Io i?i +l£r
t i*£C+i?a)C+1
Uc(s)~-^I2(s) Przyjmujemy oznaczenia:
■Rtłfił
2L
a
zatem
Ur(s\ n •Rą-+<Ł
■ cW •
Na podstawie relacji 15 z tabl. D.l otrzymujemy wartość chwilową napięcia na kondensatorze dla * > 0 w postaci:
«c(0 - Rt/o[t- (cosfc+ - sintoje--].
Po podstawieniu wartości danych, otrzymujemy
uc(t) _ 100[1—(cos280*+3sin280t)e-150*] V.
Z otrzymanych zależności widać, że napięcie na kondensatorze w stanie ustalonym wynosi /?,/<> ». 100 V. Można to łatwo wyjaśnić. W stanie ustalonym prąd przez kondensator nie płynie, a napięcie na cewce równa się zeru. Z zależności tych wynika również, że w stanie przejściowym napięcie na kondensatorze może być większe od napięcia na tym kondensatorze w stanie ustalonym. W przypadku małego tłumienia, tzn., gdy jest spełniona zależność a < b, napięcie na kondensatorze w stanie przejściowym jest większe w przybliżeniu j/L/C rmy wzglądem tego napięcia w stanie ustalonym. Dla danych wartości w zadaniu mamy a =* 150 i b — 278 rad/s i dlatego nie
wystąpią na kondensatorze znaczne przepięcia.
*
4.22. Do dwójnika szeregowego RC o warunkach początkowych zerowych (rys, a) w chwili! «= 0 zostaje doprowadzone napięcie o przebiegu przedstawionym na rys. b.
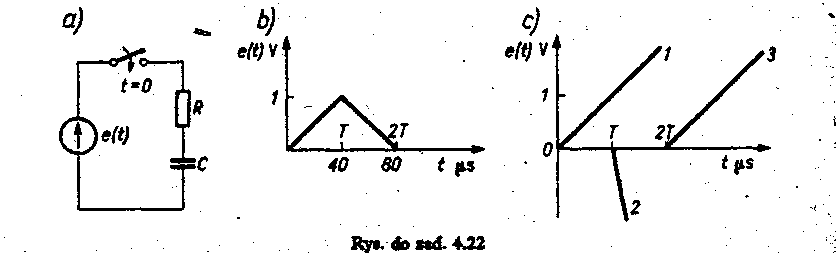
Wyszukiwarka
Podobne podstrony:
IMG141 14] W układzie symetrycznym sumy w nawiasach aa równe zeru, z czego wynika ważna własność ukł
IMGB20 (3) ośrrrtHić fcczfeę operaty (ciągów). a następnie aa podaawie tabt. 13.3 i 13 4 dobrać wip6
13852 skanuj0012 408 Rys. 14.13 Rozwiązanie Impedancja wejściowa wyrażona przy użyciu współczynnika
20688 skanuj0007 (320) 59 Ćwiczenie 5 Przyjmując rozwiązania równań (5.4) w postaci drgań harmoniczn
Widać już, że rozwiązanie (3.1) ma postać= azr=i(i-a) n-(.aibo Y,p = nY, + a(l - a)y,_, + (1 - a)2Y,
SDC16825 Reakcję w węflc wewnętrznym wyznacza się rozwiązuj*: graficznie równanie równowagi ij dział
BEZNA~49 Napięcie na kondensatorze obliczamy korzystając ze schematu obwodu w postaci operatorowej p
BHP 1h (26) Duża cześć patentowanych rozwiązań przyjmuje postać bezpośrednio użytkową dopiero po dłu
4. Rozwiąż krzyżówkę. 1. Inaczej operator filmowy. 2. Dokonuje
CCF20081211�007 Do rozdziału X 453 Do rozdziału X 453 9.102. Macierz X nie istnieje. 9.103. Ogólne r
więcej podobnych podstron