CCF20081211007

Do rozdziału X 453

Do rozdziału X 453

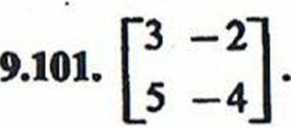
9.102. Macierz X nie istnieje.

9.103. Ogólne rozwiązanie ma postać (Ci, C₂ dowolne stałe):

TC₁ £(2-3C,)-l |_C₂ J(9-3C₂)J‘

DO ROZDZIAŁU X

10.58. x— — 6, y=— 50 maksimum; x=—4, y= — 66 punkt przegięcia; x=—2, y=

= —82 minimum.

0

Uwaga. Aby obliczyć wartość wielomianu y=x³+ \2x²+ 36x — 50 przy x=— 2, przedstawiamy wielomian w postaci y=((x+ 12)x+36) x — 50 i podstawiając x= —2 obliczamy kolejno: -2+12=10, 10(—2) = —20, -20 + 36=16, 16(-2)=-32, -32 - 50= = -82.

10.59. x — — 1, y= 1 maksimum: jc = f, y= — ^§5 punkt przegięcia; x = 4, y——124 minimum.

10.60. x=l, y = 2 maksimum; x=2, y = 0 punkt przegięcia; x = 3, y=— 2 minimum.

10.61. x = 0, y — 0 minimum; x = |, y = jj punkt przegięcia; x = |, jp=A maksimum.

10.62.    Funkcja jest stale rosnąca; x = 0, y=\ punkt przegięcia.

10.63. x = 1, j>> = 4 maksimum; x = 2, y=2 punkt przegięcia; x = 3, y = 0 minimum.

10.64.    x=\, y=3 minimum; x=2—\yj3, y=~£ punkt przegięcia; x=2, y = 4 maksimum; x = 2 + \yj3, y = ^ punkt przegięcia; x = 3, y = 3 minimum.

Uwaga. Sposób obliczania wartości wielomianu jest podany w odpowiedzi do zadania 10.58.

10.65. x = 0, y= 1 punkt przegięcia; x=|(3 —,/3), y-1(-55 + 39 _>/3) punkt przegięcia; x= 1, y = 2 maksimum; x=i(3 + _>/3)_ł ,y=|(-55-39 yj3) punkt przegięcia, x=3, y=— 26 minimum.

10.66.    Funkcja określona, gdy xj^f=0; x= — 2, y = —4 maksimum; x = 2, y = 4 minimum.

10.67.    Funkcja określona, gdy x^0; x= —1, y=2 minimum; lim y= +oo; lim y =

-    a • •    — 0    x-* + 0

= +oo; x= 1, y=2 minimum.

10.68.    x=—y/3, y=—\y[3 punkt przegięcia; x= — 1, y— — 1 minimum; x = 0, j=0 punkt przegięcia; x= 1, ,y=l maksimum; x = ^/3, y = isf3 punkt przegięcia.

10.69.    Funkcja jest określona w przedziale —2<x<2; x-—y/2, y= — 2 minimum; x = 0, ^ = 0 punkt przegięcia, w którym y' = 2; x — ^[2, y=2 maksimum.

10.71. a=-3.    10.72. a = ±2.

10.73.    Przy x= -2, y_mmx= -2; przy *=2, y_min = 2; asymptoty: y = 6 i y = \x.

10.74.    Funkcja jest określona, gdy x/4; ekstremów nie ma, gdyż funkcja jest stale malejąca; asymptoty: jc=4 i y—2.

10.75.    x=— 2, y=— 3 minimum; x~2, y=l maksimum; asymptota y = 0.

10.76.    Funkcja jest określona, gdy x^ —2 i xj^ — 1; jc= —y/2, y = — 17—12 y/2 maksimum; jc = _n/2, y= — 17+12 yjl minimum: asymptoty: x=— 2, x=— 1, y= 1.

10.77.    jr = 0, y= —1 minimum; x = 2, _y = | maksimum; asymptota y=l.

10.78.    x~ — 1. y——2 minimum; x=\, y = 2 maksimum; asymptota y = 0.

(x +2)³(x —2)

10.79. Funkcja jest określona, gdy xź -1; y =-_z— ; x= -2, y = 0 maksi-

(x+l)

mum; x = 2, y =    minimum; asymptoty: x—— 1, ;> = jc-ł-5.

10.80.    Przy x = l, y_mkK= -4; przy x = 5, y_min = 4; asymptoty; jc = 3, y = x-3.

10.81.    Przy    7m.* = n-1 %2,14; przy = -irc, y_min= 1 -k^-2,14; asymptoty

10.82.    / = 3(x + |) (x —2), y" = 6x + 2 (rys. R. 10.1); tabelka(‘):

X	— 00	• • •	8 ~ 3	• • •	i ”3	• • •	2	...	+ OO
/'	— 00	—	—	—	0	+	+	+	+ 00
y'	+ OO	+	0	—	—	—	0	+	+ 00
y	— OO		398 27 M	\	286 27 P	\	-36 m	/	+ OO

(*) W tabelce symbol M oznacza maksimum, m — minimum, p — punkt przegięcia.