2

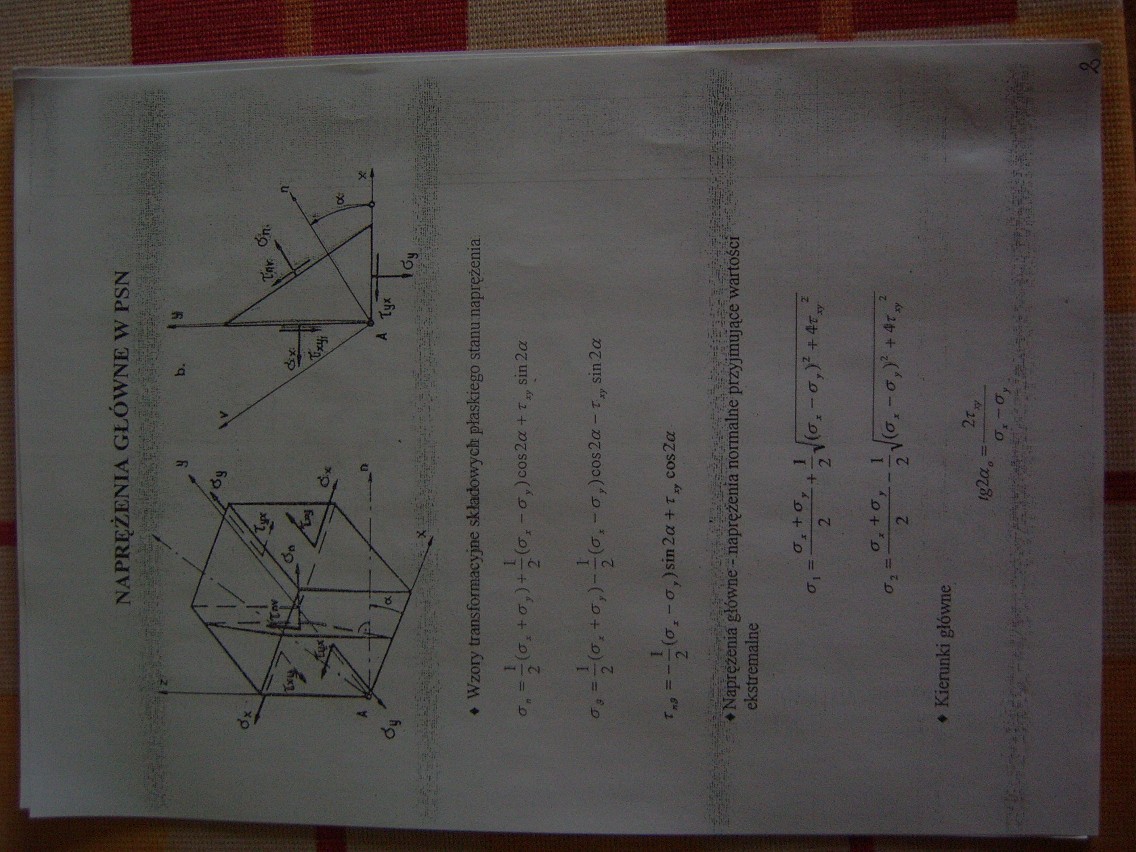
NAPRĘŻENIA GŁÓWNE W PSN

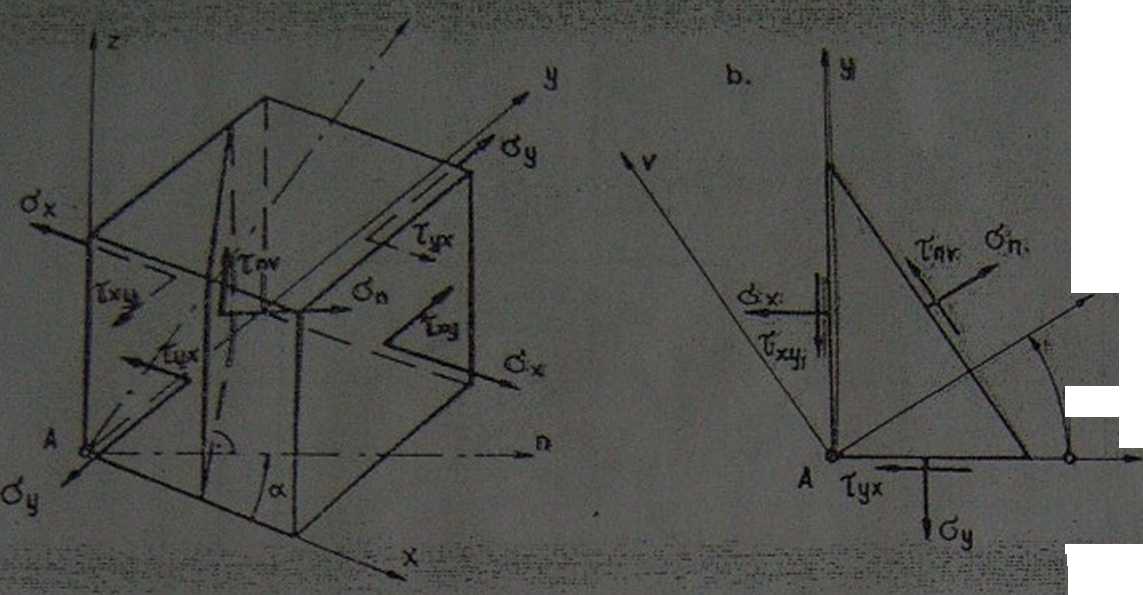
♦ Wzory transformacie składowych płaskiego stanu naprężenia

⁺    ” ^cr.y)cos2a + r_xy sin 2or

^ =|(cr, +c7_>.)-~(<7, -cr_v)cos2a- r^sinża

= - — (er, - <J_r)sin2a + r_xy cos2cc

♦ Naprężenia główne - naprężenia nonnalne przyjmujące wartości ekstremalne

<7*+<r_r I r---

'■=-o-⁺-V(^“^crr>

-f 4r

■*y

a + (7 i i--;--

^ffa=-V-^Ł-    + *V

♦ Kierunki główne

2r

®2a..«--* -

er - a..