6 7

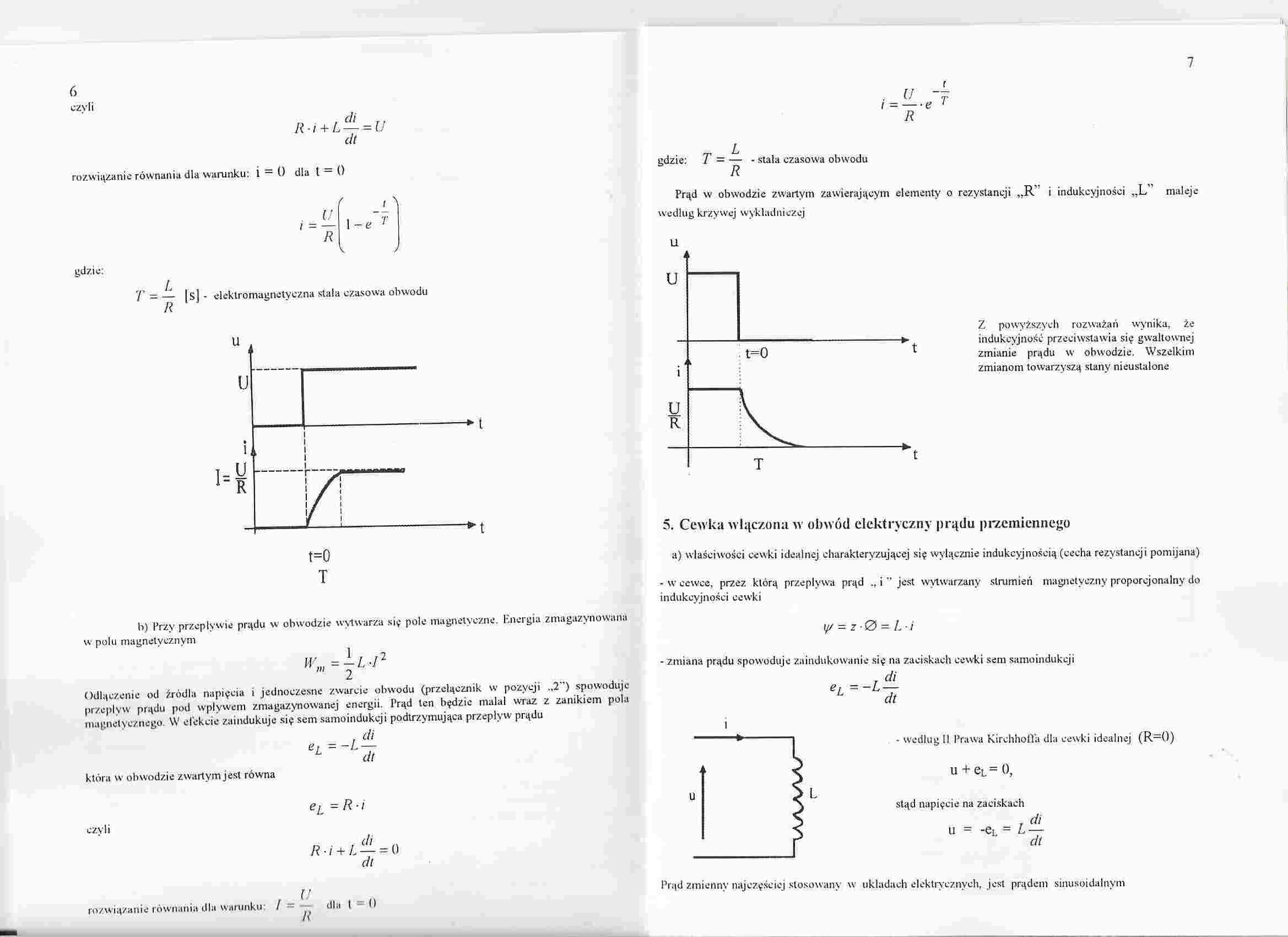
rozwiązanie równaniu dla warunku: 1 — 0 dla t — 0

r

- e

(

_u_

' ~ R

\

gdzie:

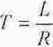
|s] - elektromagnetyczna stała czasowa obwodu

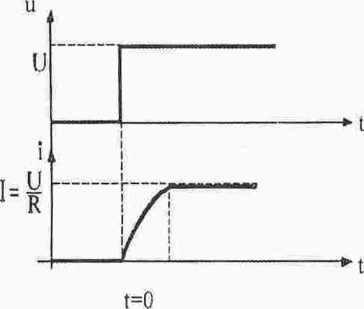
T

h) Przy przepływie prądu w obwodzie wytwarza siy pole magnetyczne. Energia zmagazynowana u polu magnetycznym

Odłączenie od źródła napięcia i jednoczesne zwarcie obwodu (przełącznik w pozycji ..2") spowoduje przepływ prądu pod wpływem zmagazynowanej energii. Prąd len będzie malał wraz z zanikiem pola magnetycznego. W elekcie zuindukuje się sem samoindukcji podtrzymująca przepływ prądu

di

e, = -L —

^L dl

która w obwodzie zwartym jest równa

^eL = R’i

czyli

R • i + L — = 0 dl

^f dla l = 0

R

rozwiązanie równania dla warunku /

. U

f

T

i = —e ¹ R

udzie: T — — - siała czasowa obwodu

R

rezystancji ,JR i indukcyjności ,,L’ maleje

Prąd w obwodzie zwartym zawierającym elementy

według krzywej wykładniczej U

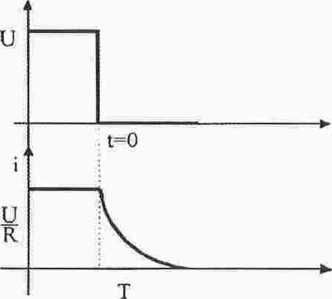
Z powyższych rozważań wynika, że indukcyjność przeciwstawia się gwałtownej zmianie prądu w obwodzie. Wszelkim zmianom towarzyszą stany nieustalone

5. Cewka wleczona w obwód elektryczny prądu przemiennego

a) właściwości cewki idealnej charakteryzującej się wyłącznie indukeyjnością (cecha rezystancji pomijana)

- w cewce, przez którą przepływa prąd i " jest wytwarzany strumień magnetyczny proporcjonalny do indukcyjności cewki

I// = z • 0 = L i

zmiana prądu spowoduje zaindukowanio się na zaciskach cewki sem samoindukeji

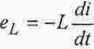
I

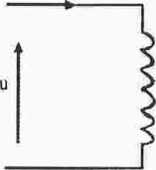
- według II Prawa Kirchhoila dla cewki idealnej (R—0) U + e_L= 0,

stąd napięcie na zaciskach

di

u = -ei = L — dt

Prąd zmienny najczęściej stosowany w układach elektrycznych, jest prądem sinusoidalnym