9 06

Nagrzewanie elementów aparatów

Z powyższych warunków wynika, żc

A,    = A₂ = 2 (*>»-*>>.); b, = o

B,    = ^(^-W^sinlifr.,),*.

Po podstawieniu i przekształceniach

f>, = (0„-0,„)cosh(a₁).jt + d₁„    (2.75)

,% = ^-(i>₁.-»Jc-<*->2<-*.»sinh(a_l)i^+^2.    (2.76).

V*l/2

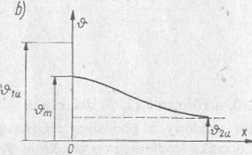
Rys. 2.44. Tor prądowy z podwójną zmianą przekroju: a) rysunek toru, b) rozkład temperatury

Maksymalna temperatura występuje dla x = 0 i wynosi

»m =    ------- (2.77)

cosh(a,), x„ + sinh(a,),.r₀ \Pl/2

Przykładowy przebieg temperatury przedstawiono na rys. 2.44b. Z powyższych wzorów wynika, żc na wartość ■&„ można wpłynąć np. przez zmianę długości x₀.

D. Rozpatrzony zostanie przypadek toru prądowego częściowo izolowanego (rys. 2.45). Tor prądowy o stałym przekroju S na odcinku o długości 2x₀ pokryty jest izolacją. Przebieg obliczania będzie analogiczny jak w przypadku C, z tym że dla odcinka izolowanego inne będą wartości współczynników a_x i a₂.

Dla izolowanej części przewodnika strumień cieplny odprowadzany z powierzchni zewnętrznej do otoczenia przechodzi przez warstwę izolacji, wywołując w niej spadek temperatury. W wyrażeniach na a₂ i a₂ zmianie ulega człon kA> który dla przewodnika o przekroju kołowym powinien być zastąpiony odpowiednim składnikiem wzoru (2.56)

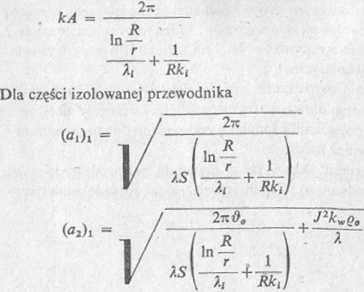
Oznaczenie jak do wzoru (2.56) oraz na rys. 2.45.

(2.78;

(2.79;

I

I

I

I

2

a)

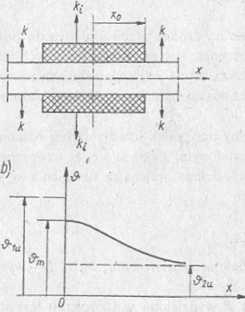
Rys. 2.45. Tor prądowy o stałym przekroju, częściowo izolowany: a) rysunek toru, b) rozkład temperatur

Wartości współczynników (a_x)₂ i (^2)2 dla części nieizolowanej prze wodnika wyznacza się zgodnie ze wzorami (2.37).

Wyrażenia na rozkłady temperatur oraz temperaturę maksymalną będ identyczne jak wzory (2.75), (2.76) i (2.77) pod warunkiem obliczania {aCii i (a₂) wg wzorów (2.78) i (2.79). Rozkład temperatury na długości przewodnika (ry 2.46b) ma podobny charakter jak w przypadku C (rys. 2.44b).