CCF20101004012

34

2. Ocena, błędu maksymalnego

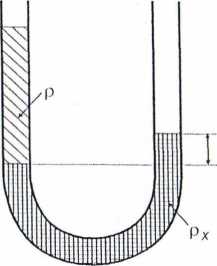
Rys. 2.3: Naczynia połączone z cieczami nie mieszającymi się

[ hx

0.2 mm, wobec l.ego Ah — Ali_x = 0.2 inrn. Przyjmując, że znamy dokładną. wartość gęstości wody (Ap = 0) otrzymujemy: p_x = 13.3088 g/cm'¹, Ap_x/p_x = 0.01054, Ap_x = 0.14027 g/cm³. Zaokrąglając błąd względny mozolny powiedzieć, żc gęstość rtęci została wyznaczona z dokładnością 1.1%. Zgodnie z tym, co powiedziano w rozdziale 1.1.4, wynik zapiszemy w postaci:

p_x = (13.31 ± 0.15) g/cin³.

3. Wielkości charakteryzujące serię pomiarów obarczonych błędami przypadkowymi

W poprzednim rozdziale przedstawiliśmy ocenę błędu maksymalnego, która umożliwia uwzględnienie błędów systematycznych. W tym i trzech następnych rozdziałach będziemy rozpatrywać przypadki, gdy błędy systematyczne można pominąć w porównaniu z błędami przypadkowymi. Bę- | dziemy więc rozważali przypadki, gdy wykonujemy serię pomiarów i rozrzut | wyników będzie znacznie większy niż dokładność przyrządu pomiarowego. | lOtżda seria pomiarów zawiera skończoną liczbę wyników N. W praktyce | liczba wyników pomiarów N wynosi od kilku do kilkudziesięciu, jest więc | liczbą niezbyt dużą. W związku z tym, zanim przejdziemy do omówienia. * tych najprostszych zagadnień statystyki matematycznej, które mająbezpo-śrcd nic zastosowanie praktyczne przy ocenie błędu i przedstawianiu wyników pomiarów, zajmiemy się, zarówno w przypadku pomiarów bezpośrednich, jak i pośrednich, wielkościami wyznaczanymi na podstawie wyników pomiarów charakteryzującymi serię pomiarową.

3,1. Wartość średnia serii pomiarów bezpośrednich

W rozdziale ]. 1.5 pokazaliśmy, że błędy przypadkowe powodują rozrzut wy- I iiików pomiaru, tzn. że jeżeli wykonamy serię /V pomiarów tej samej wiel- g kości fizycznej x, to otrzymamy ciąg jej wartości x i, x₂,..., x/v• Wartości te ! będą rozłożone w pewnym przedziale, tzw. przedziale zmienności. ,J ak I wykazuje praktyka pomiarowa (i co będzie dalej uzasadnione) rozrzut wyni- 1 ków nie jest równomierny. Przy dużej liczbie pomiarów widać, że układają ! się one w pobliżu pewnej wartości a, leżącej wewnątrz przedziału zmienności- Przykład takiego rozrzutu przedstawiono na. rysunku 3.1. W związku z występowaniem rozrzutu wyników pomiaru w pierwszej kolejności podamy kryterium, które pozwoli znaleźć wartość a, wokół której grupują się wyniki | serii pomiarów.

Najprostszym narzucającym się kryterium jest założenie, że suma wartości bezwzględnych różnic między poszukiwaną wartością a ora.z wynikami