CCF20101004009

20 2. Ocena, błędu maksymalnego

długość pręta liczbę kiesek podział ki liczymy zmuszę poczynając od kreski przyjętej za zero. Z tego powodu jedyną niepewnością jest ustalenie czy kreska przyjęta za zero pokrywa się z początkiem pręta. Jeżeli patrzymy prostopadle, a więc możemy pominąć błąd paralaksy, to niepewność pokryciu. się kreski przyjętej za zero b początkiem pręta nic będzie większa niż grubość kreski. Zazwyczaj grubość kreski nic przekracza 2/10 odstępu między kreskami, a więc błąd spowodowany grubością kreski jest znacznie mniejszy niż błąd maksymalny i dlatego go pomijamy. Należy podkreślić, żo. wnioski wynikające z tego przykładu są prawdziwe wtedy, gdy pomiar wykonujemy prawidłowo.

2) 7,a pomocą śruby mikrometrycznej mierzymy średnicę drutu.

Jeżeli śruba jest wykonana prawidłowo, tzn. skok gwintu jest stały (zmiana, skoku gwintu powoduje, że jeden obrót śruby będzie się różnił od drugiego) i kreski podziałki na ruchomym bębnie są naniesione w jednakowych odstępach, oraz nic występuje przesunięcie zera, to wtedy, gdy skok śruby wynosi 0.5 mm i bęben podzielono na 50 części, dokładność śruby i zarazem błąd maksymalny wynosi 0.01 mm. Jeżeli w tej samej śrubie bęben podzielono na. 25 części, dokładność wynosi 0.02 min. Gdy zmierzona wartość średnicy drutu wynosiła. 2.54 mm, wynik odczytu w pierwszym przypadku zapiszemy d = (2.54 i 0.01) mm, a, w drugim d = (2.54 ± 0.02) mm.

|~Na, zakończenie należy podkreślić, że jeżeli przyrządy są sprawne i wykonane prawidłowo, a pomiary wykonujemy poprawnie, to błąd przy odczycie skali, równy dokładności przyrządu, jest błędem systematycznym dla pomiarów wykonanych tym przyrządem. Jest to jednocześnie błąd maksymalnej Wykonując pomiary bezpośrednie często stajemy przed pytaniem: czy błąd systematyczny spowodowany dokładnością przyrządu pomiarowego jest mniejszy, czy też większy od błędów przypadkowych? Odpowiedź możemy uzyskać powtarzając pomiary. Jeżeli wykonamy serię pomiarów i rozrzut otrzymanych wyników jest w granicach dokładności przyrządu pomiarowego, i.o będzie to oznaczało, że błąd systematyczny jest większy niż błędy przypadkowe. Na przykiad mierzymy natężenie prądu, dokładność amperomierza wynosi 0.2 A i otrzymujemy wartości 3.2 A, 3.1 A, 3.2 A, 3.3 A — rozrzut wyników jest więc zawarty w granicach dokładności amperomierza.

W praktyce (nie tylko laboratoryjnej) pomiary wielkości nieelektrycznych zastępuje się pomiarami wielkości elektrycznych stosując odpowiednie przetworniki, a. mierniki elektryczne wskazówkowe są coraz częściej zastępowane miernikami cyfrowymi. Wydawałoby się, że skoro wynik pomiaru otrzymujemy w postaci cyfrowej, to jest on bezbłędny. Tak w rzeczywistości nie jest.fiJokladność mierników cyfrowych jest większa niż w innych ; typach mierników, tym niemniej pomiary wykonane przy icli użyciu są także

obarczone błędami. Nie wnikając w zasady działania mierników cyfrowych możemy przyjąć, że dokładność ich jest równa sumie dokładności wskazania i dokładności zakresu pomiarowegojDokladności te zależą od rodzaju wielkości mierzonej i są z reguły podawane, w instrukcji tniernika.jjw przy- | pad ku braku tych danych musimy przyjąć, że błąd jest równy e.) najmniej | jedności na ostatniej cyfrze wynika odczytanego z miernikaJ

2.2. Oszacowanie błędu maksymalnego w pomiarach pośrednich, metoda różniczki zupełnej

Metoda oszacowania błędu wielkości złożonej przedstawiona poniżej do- | tyczy przypadków, gdy błędy systematyczne pomiaru wielkości mierzonych | bezpośrednio są znacznie, większe niż błędy przypadkowe, lub gdy wielkości | lc zostały zmierzone jeden raz (jak to jest przy pomiarach kalorymetrycz- | nycli), w tych przypadkach bowiem nie można stosować metod stal.ystycz- I nycli. Zgodnie z tym co powiedziano w rozdziale 2.1 musimy przyjąć, że | pomiary wykonane jeden raz są obarczone błędem równym dokładności 1 przyrządu pomiarowego.

Jlląd pomiaru pośredniego jest zależny od błędów wielkości mierzonych bezpośrednio. W związku z tym w przypadku oceny błędu w pomiarach ..„ćrnrlnirh svtuac.ia iest bardzie i złożona. W celu uzyskania wiekszei orzei- tł

z = f{x,y)

(2.2.1)

Odpowiada to np. wyznaczaniu przyspieszenia ziemskiego g za pomocą wah ad la matematycznego na podstawie wzoru (1.1.3), gdzie g = f(l,T). Oznaczmy przez Xq i yo wartości rzeczywiste wielkości x oraz y, a przez x_m i ij,n wartości otrzymane z pomiaru wielkości fizycznych x i y. Odpowiednio niecił Aa; i Ay oznaczają błędy maksymalne zmierzonych wartości x_m i y_m. yVart()ść rzeczywistą wielkości złożonej z oznaczmy przez zo, zaś wartość wyznaczoną na podstawie pomiarów wielkości x oraz y przez z,„. Ponieważ Z = l(x,y), to z„ = /(.x'y, t/«) oraz zakładamy, że z_m = f(x_rn,y_m). yyobec tego wartość bezwzględna różnicy z_m — zo^:

(2.2.2)

hm “Zol =    /(*0,!/o)l

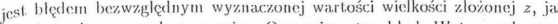
i.j,,, jest obarczony dany pomiar. Uszanujmy ten Dląd. w tym celu roz-wińmy funkcję f(x,y) na szereg Taylora funkcji dwu zmiennych w otoczeniu punktu (x_m,y_m) i obliczmy jej wartość w punkcie (,t_u, y₀) (o rozwijaniu