CCF20101004010

30 2. Ocen a błędu maksymalnego

Postawiając (2.2.8) do (2.2.7) otrzymujemy:

km - *ol < Aa =

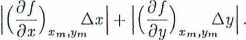
(2.2.9)

Wzór (2.2.9) można bardzo łatwo uogólnić na przypadek, gdy wielkość złożona ^ jest funkcją, r wielkości mierzonych bezpośrednio, tzn. z = f(xi, *2, • •., £_r). Oznaczmy przez z_m|i, z_m|2,..., z_m,_r wartości zmierzone wielkości aą, • • •, &_r» ^a przez Asą, A.t₂,..., Ax_r ich błędy maksymalne. Wykonujące rachunki identyczne jak powyżej otrzymujemy:

(2.2.10)

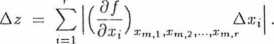
Wyrażenie (2.2.10) pozwalające oszacować błąd maksymalny wielkości złożonej stanowi ilościowe ujęcie tzw. reguły przenoszenia błędu dla przypadku błędu maksymalnego. Przedstawiona metoda obliczania błędu maksymalnego często nosi nazwę metody różniczki zupełnej.

Ze wzoru (2.2.G) wynika, że:

— Az < zq < z_m Az.

(2.2.11)

Otrzymujemy więc związek analogiczny do nierówności (1.1.4). Możemy go również przedstawić w formie wzoru (1.1.7), tj.:

z₀ = z_m ± Az .

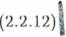
We wzorach (2.2.11) i (2.2.12) z_m = f(x_m)y_m) odpowiada x we wzorach (1.1.4) i (1.1.7), zaś błąd maksymalny A z odpowiada A we wzorach (1.1.4) i (1.1.7). W ten sposób, w przypadku gdy błędy systematyczne są znacznie większe od przypadkowych, lub gdy jakakolwiek wielkość fizyczna mierzona bezpośrednio została zmierzona jeden raz, otrzymaliśmy odpowiedź na pytanie postawione w rozdziale 1.1.2 o cel teorii błędów.

Należy zaznaczyć, że jeżeli błędy maksymalne wielkości mierzonych bezpośrednio Azostały określone prawidłowo i nie ma innych źródeł błędów systematycznych, to wielkość Az obliczona ze wzoru (2.2.10) określa gra.-nicc (górną, i dolną.) przedziału, w którym zawarta jest wartość rzeczywista.

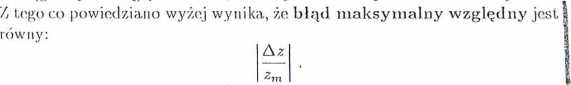
Na zakończenie tego rozdziału przedstawimy przypadek, kiedy zastosowanie metody różniczki zupełnej umożliwia bardzo proste obliczenie błędu

maksymalnego względnego. Niech wielkość złożona z będzie funkcją wielkości mierzonych bezpośrednio z, (i = 1,2,..., r) postaci:

r

z = /lIK'.    (2.2.13)

i=l

gdzie A oraz a, są stałymi. Logarytmując równanie (2.2.13) otrzymujemy:

(2.2.14)

ln z = In A Y, a, In z,.

Korzystając ze znanego wzoru d(ln }(x)) = d (/(i))//(z) i założeń zrobionych przy wyprowadzeniu wzoru (2.2.10) otrzymujemy dla błędu względnego wyrażenie:

(2.2.15)

£l-śl«£l-

Ten sposób obliczania błędu maksymalnego względnego bywa nazywany metodą pochodnej logarytmicznej.

Ze wzorów (2.2.10) i (2.2.15) wynikają podstawowe reguły przenoszenia błędów maksymalnych, a mianowicie jeżeli:

1. z = xy a.'2 to Az = |A.i;i| T |Ax2].

2. z = xy - X‘i to Az = | A:c 11 + | Am^j].

3.    z = r.ix₂ to Az/z = lAzi/z,! 3- |A.r₂/a:₂|.

4.    z = x,/x₇ to Az/z = |Axi/zi| + |A.x-₂/a:₂|.

Z powyższego wynika, że: jeżeli wielkość złożona z jest sumą lu > różnicą wielkości mierzonych bezpośrednio, to dodają się błędy maksymalne, a gdy iloczynem lub ilorazem to dodają się błędy maksymalne względne.

Przykłady

1.    Wyznaczanie obwodu czworokąta.

Mierząc boki czworokąta otrzymujemy wartości /₂, /_;!, Ią. Obwód czworokąta. L r= ly -|- /₂ -|-    /.,. Niech błędy maksymalne pomiarów boków

tego czworokąta wynoszą A/|, A/₂, Al-j i AIą. Wówczas błąd maksymalny wyznaczonego obwodu będzie AL — Alt -|- A/₂ -I- A/_:) + A/,₍. W przypadku gdy A/₍ = A/₂ — A/;j = Al,| = A/ to Ab = 4A/; czyli błąd wyznaczonej długości obwodu czworokąta będzie czterokrotnie większy niż błąd pomiaru każdego z boków.

2.    IVijziwczani.e. ciepła topnienia lodu.

Ciepło topnienia lodu wyznaczamy przy użyciu kalorymelru wodnego. Oznaczmy odpowiednio przez cjt, m-i- i c,„, rn„, ciepło właściwi' i masę kalorymel.ru z mieszadeł kiom oraz ciepło właściwe i masę