CCF20101004015

3. Wielkości cli arak teryz ujące serię pomiarów..

Wysumujmy błędy bezwzględno i podzielmy przez licz,bę pomiarów. Otrzymamy wtedy:

1 N    i ^N

77 E-⁵- = 77 J2^xi-*o-    (3.2.5)

i=l    i=l

Z powyższego równania wynika, że

z₀

N ■

N    . N

J2^xi - ^E'⁵- =

(3.2.0)

gdzie

(3.2.7)

Ponieważ nie mamy żadnych podstaw, aby przyjąć, że x jest równe x₀, musimy przyjąć, że w ogólnym przypadku x yź x₀ więc i <1    0. Podstawiając

(3.2.6) do (3.2.4) otrzymujemy:

Si = Xi — £ + 5.

Stąd:

Xi-£ = 5i-6.    (3.2.8)

Podnosząc (3.2.8) obustronnie do kwadratu, sumując po i (i = 1,2,..., /V) oraz dzieląc przez liczbę pomiarów mamy:

yv

/V

^    = ^X>* + («)^ł(3.2.9)

t= L    t = l    t=J    *=1

Wstawiając (3.2.7) do (3.2.9) i biorąc pod uwagę wzór (3.2.3) otrzymujemy: £><-*)* =

/V

;Y

(3.2.10)

i=l

Ale

w^j = (*£»’ -    («■")

' t=l    i=l    J

Ponieważ iloczyny SjSk U i- fc) mają różne znaki, nie popełnimy dużego błędu, jeżeli dokonamy przybliżenia i pominiemy w równaniu (3.2.11) wyraz zawierający te iloczyny. Otrzymamy wtedy:

{Śf

\    "    i

E# = —si.

N'¹ <

N ^x '

(3.2.12)

I

Podstawiając (3.2.12) do (3.2.10) znajdujemy:

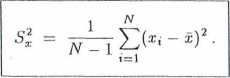
(3.2.13)

Otrzymane wyrażenie zawiera jedynie wielkości będące wynikiem pomiaru, pozwala więc na obliczenie odchylenia standardowego serii S_x. Występująca w mianowniku wzoru (3.2.13) liczba N -1 = k jest nazywana liczbą stopni swobody. Jest ona równa liczbie niezależnie wyznaczonych wielkości (liczbie pomiarów) minus liczba wielkości (parametrów) obliczonych przy ich użyciu. W naszym przypadku jest jedna wielkość obliczona na podstawie serii N pomiarów, jest nią średnia arytmetyczna x, która jest niezbędna do obliczenia S_x. Inaczej mówiąc liczba stopni swobody k — N — Q, gdzie N jest liczbą niezależnie wyznaczonych wielkości, aQ liczbą równań wiążących te wielkości.

Odchylenie standardowe serii S_x charakteryzuje precyzję wykonania po- f miarów w danej serii pomiarowej i możemy je uważać za średnią wartość | niepewności każdego z pomiarów danej serii pomiarowej. Błędy poszczegól- f nyc.h pomiarów przenoszą się na obliczoną wartość średniej arytmetycznej | X. Wielkość charakteryzującą precyzję wyznaczonej średniej arytmetycznej i ■x nazywamy odchyleniem standardowym średniej arytmetycznej 1 serii S_x\ obliczymy je w rozdziale 3.4, w którym poznamy „regułę przeno- I szenia. błędów” w przypadku, gdy wyniki pomiarów niezależnych obarczone 1 są błędami przypadkowymi.

3.3. Wartość średnia serii pomiarów pośrednich

W dwóch poprzednich rozdziałach, dla mierzonej bezpośrednio wielkości fizycznej x, znaleźliśmy wartość, wokół której grupują się wyniki pomiarów, tj. średnią arytmetyczną x oraz odchylenie standardowe serii 5*. Większość wielkości fizycznych to wielkości złożone, zależne od wielkości mierzonych bezpośrednio. Ich pomiar jest pomiarem pośrednim i został on wyjaśniony w rozdziale 1.1.1. Dla łatwiejszego zrozumienia i większej przejrzystości rozważań przyjmijmy, że wielkość złożona z jest zależna od dwóch mierzonych bezpośrednio wielkości x i y, tzn., że

Z = /(*,.’/)■    (3.3-1)

3.3.1. Pomiary niezależne

Zalóżm y, że obie mierzono wielkości fizyczne s«( od siebie całkowicie nieza-leżi le, to znaczy, że wynik pomiaru jednej wielkości nie zależy od wyniku

'.. a?    aj