CCF20101004013

38 3. Wielkości charakteryzujące serię pomiarów...

stąd zaś mamy zależność (3.1.3) oraz

38 3. Wielkości charakteryzujące serię pomiarów...

Ostatecznie otrzymujemy:

Z analizy matematycznej wiadomo, że warunek zerowania się pierwszej

W dalszym ciągu tego opracowania wszędzie Lam, gdzie będziemy poszukiwali ekstremum funkcji, ograniczymy się do znajdowania miejsc zerowych

pochodnej funkcji, której ekstremum poszukujemy, jest warunkiem koniecznym, ale niewystarczającym. Jak łatwo się przekonać, w przypadku funkcji Aj\r(a) w punkcie u. danym wzorem (3.1.7), znajduje się jej minimum.

pierwszej pochodnej. We wszystkich tych przypadkach będą to ekstrema, a nie punkty przegięcia. Sprawdzenie tego pozostawiamy czytelnikowi.

Wielkość o., wokół której grupują się wyniki pomiarów obarczonych błędami przypadkowymi, dana równaniem (3.1.7), jest niczym innym i^a^ średnią arytmetyczną x wartości 2; (i = 1, 2,..., N), czyli

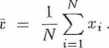
(3.1-8)

Związek średniej arytmetycznej x, wokół której grupują się wyniki serii

N pomiarów obarczony ctr-ldędami przypadkowymi z wartością rzeczywistą omówimy w rozdziale 5.

W ogólności średnią arytmetyczną dowolnych wielkości nazywamy ^1C^' sumę podzieloną przez ich liczbę.

Oprócz średniej arytmetycznej zdefiniowane są inne średnie, jak np.:

■ średnia kwadratowa    _

\ ’

śród ii i a h ar moniczn a

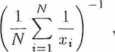
ś ret Inia geo i n e 1. rycz 11 a

W dalszym ciągu wykładu będziemy spotykali się z średnią arytmetyczną i średnią kwadratową.

Warunek (3.1.')) pozwala na jednoznaczne wyznaczenie wartości, wokół której grupują się wyniki pomiarów. Wyznaczone ze wzoru (3.1.7) wartości średnich arytmetycznych dla uprzednio podanych przykładowych serii pomiarowych wynoszą odpowiednio: 11.125 w przypadku 4 pomiarowi 11.000 w przypadku 5 pomiarów.

Zatem w celu znalezienia wartości, kolo której grupują się wyniki pomiarów, szukamy takiej wartości n, dla której suma kwadratów różnic z,— a jest najmniejsza. Poszukiwanie wartości, dla której jakieś wyrażenie ma wartość najmniejszą nazywa się minimalizacją. Przedstawiony sposób minimalizacji nosi nazwę metody najmniejszych kwadratów. Postępowanie polegające na. wykorzystaniu warunku (3.1.4) w celu znalezienia wartości u, na podstawie wyników pomiarów jest najprostszym przykładem zastosowania metody najmniejszych kwadratów. Do metody tej wrócimy w rozdziale 3.5 i rozdziale 5.

Wzór (3.1.8) pozwala nam obliczyć średnią arytmetyczną serii pomiarów zawierającej /V wyników. Często zdarza się, że chcemy znaleźć wartość średnią z różnych serii pomiarowych tej samej wielkości fizycznej x. Przypuśćmy, że wielkość fizyczna. x była zmierzona w I. seriach pomiarowych o jedn akowej precyzji. Każda z serii pomiarowych miała inną średnią Xk (h = 1,2i w każdej z serii wykonano inną liczbę pomiarów Nk-Znamy tylko xk i ^k_} nie znamy natomiast wyników poszczególnych pomiarów wykonanych w każdej serii. Dla każdej z serii zgodnie z definicją średniej arytmetycznej spełniony jest związek Nk^xk = ^x*j- Możemy więc znaleźć układ L równań:

Ni

^N'^Sl ~

3 = 1 Nr

N₂x₂ =    (3.1.9)

i=l

N l.

Nlxi. = ^x,-i ■ j=1

Dodając do siebie stronami powyższe równania otrzymujemy:

/,    7V,    N₂    N_l

^kik ~ 5Ż + Yi ^x'br + • • • + X. ^x<;3 ■

k=l    j = 1    j=i