CCF20101004016

'18 3. Wielkości charakteryzujące serię pomiarów...

Korzystając z „reguły przenoszenia, błędów” (3.4.8) znajdziemy teraz odchylenie standardowe średniej arytmetycznej serii N pomiarów bezpośrednich. Zgodnie ze wzorem (3.1.8) średnia arytmetyczna jest funkcją wyników wszystkich N pomiarów, możemy to zapisać:

1 ^N

x = f(x i,ij,...,i») = — Y_,Xi.    (3.4.9)

Zgodnie ze wzorem (3.4.8) i (3.4.9) Sj jest

(3.4.10)

Wszystkie wartości S_Xi są sobie równe, ponieważ jest to odchylenie standardowe serii i jest stale dla danej serii. Aby obliczyć S_x musimy obliczyć pochodne dxldx_t. Różniczkując (3.4.9) względem z, otrzymujemy dx/dx{ = 1 /N, czyli że wszystkie pochodne są równe sobie. Wobec tego wzór (3.4.10) przyjmie postać:

Si =

N²

NS.

A więc odchylenie standardowe średniej arytmetycznej serii po-: rniarów wielkości mierzonej bezpośrednio jest dane wzorem:

■>

Si =

S_x

y/N’

(3.4.11)

Wzór (3.4.8) wyraża    ..odchyliaiiaJŁtaild^

J&MU|).QŚr(id,njift)u UJędy . lHzyji.uikowo wielkości mierzonych bezpośrednio przenoszą się, jak przedstawiono powyżej, na ich wartości średnic, zaś błędy średnich arytmetycznych tych wielkości przenoszą się na wartość z = /(z,, x₂, ..., .T_r)• Tak więc, podobnie jak w przypadku pomiarów bezpośrednich, miarą precyzji wyznaczenia wartości z będzie .S~-^Obliczymy teraz odchylenie standardowe wartości średniej serii pomiarów pośrednich Sź. W tym celu skorzystamy z przybliżonej zależności z = f(xi, x₂₎ • • •» *?•)• W związku z tym znaleziona wartość Sz będzie dotyczyła wartości ż danej przybliżonym wzorem (3.3.6), a nie wzorem (3.3.2). Dla uproszczenia rachunków przyjmijmy, że z — f(x₁y)• Wtedy, zgodnie z wzorem (3.3.5) z = /(®,jjf), oraz pamiętając, że x i y wyrażają się wzorami:

= yy (-¹'¹ + ^X2 +

+ X_N)

y = aj-(v>⁺w + -

. -I- VM) , (3.4.12)

mamy:

z = f(x[xi, X2,, XN),y{yi,yi,.. -    •    (3.4.13)

Aby obliczyć, pochodne Oz/dxi i dz/dyk musimy we wzorze (3.4.8) uwzględnić to, że funkcja z jest funkcją, złożoną. Otrzymamy wówczas:

(3.4.14)

5-2 _ -y(2ŁiL_s )² ₊ y'(°L°jL_s j^{2 2} - ^\d-xdxh>    *'

Ponieważ dx/dxi = \/N i ihj/dyk = 1/M, zaś S_x, = S_Xi = •-■== S_XN '= 6’* oraz S_yi = S_y2 = ■ ■ ■ = S_VM = S„ a więc wzór (3.4.14) możemy zapisać:

- (^dA	^2 sl +	(df>	2 S^2r °y
\dx'	i.yN		^Jx,y M
wzoru (3	.4.11) otrzymujemy:
! (Of	Y si+		Y ^ss
\dx	' *,y	W	>1,S V

(3.4,15)

(3.4.16)

W przypadku gdy wielkość złożona z jest funkcją r niezależnych wielkości mierzonych bezpośrednio x.\, X2,.. •, x_r, wzór (3.4.16) przyjmie postać:

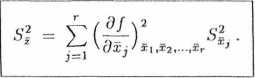
(3-4.17)

3.4.2. Pomiary zależne

Przejdziemy teraz do obliczenia odchylenia standardowego serii pomiarów pośrednich, gdy wielkości mierzone bezpośrednio są zależne. Podobnie jak w przypadku wielkości niezależnych przyjmijmy, że wielkość złożona z jest funkcją dwóch zależnych wielkości mierzonych bezpośrednio, tzn. z = f(x, y). Przyjmijmy również, że wykonaliśmy N pomiarów wielkości x oraz y i otrzymaliśmy /V par (i,, ty;) (i = 1,2,..., N) wyników pomiarów i N odpowiadających im wartości z; = f(Xi,yi) (i = 1,2,..., N). W tym przypadku wariancja serii pomiarów pośrednich S₂, zgodnie z definicją (3.2.3), wyraża się wzorem:

I ^N

^Sl = Jj X>.' - *o)^a ■    (3-4.18)

Różnicę Zj - z₀ obliczamy, podobnie jak w przypadku pomiarów nienależnych (patrz rozdział 3.4.1), korzystając z rozwinięcia funkcji z = f{x,y)