CCF20101004013

38 3. Wielkości charakteryzujące serię pomiarów...

stąd zaś mamy zależność (3.1.3) oraz N

(X>.)

«a = 0.

(3-1.6)

Ostatecznie otrzymujemy:

(3.1.7)

«= -2>.

Z analizy matematycznej wiadomo, że warunek zerowania, się pierwszej pochodnej funkcji, której ekstremum poszukujemy, jest warunkiem koniecznym, ale niewystarczającym. Jak łatwo się przekonać, w przypadku funkcji /l/v(«) w punkcie a danym wzorem (3.1.7), znajduje się jej minimum. W dalszym ciągu tego opracowania wszędzie tam, gdzie będziemy poszukiwali ekstremum funkcji, ograniczymy się do znajdowania miejsc zerowych pierwszej pochodnej. We wszystkich tych przypadkach będą to ekstrema, a nie punkty przegięcia. Sprawdzenie tego pozostawiamy czytelnikowi.

Wielkość o, wokół której grupują się wyniki pomiarów obarczonych błędami przypadkowymi, dana równaniem (3.1.7), jest niczym innym jak średnią arytmetyczną x wartości 2; (i = .1,2,..., /V), czyli

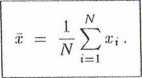
(3.1.8)

Związek średniej arytmetycznej z, wokół której grupują się wyniki serii N pomiarów obarczonyctnbłędami przypadkowymi z wartością rzeczywistą omówimy w rozdziale 5.

W ogólności średnią arytmetyczną dowolnych wielkości nazywamy ich sumę podzieloną przez ich liczbę.

Oprócz średniej arytmetycznej zdefiniowane są inne średnie, jak np.:

średnia kwadratowa

1 ^N

-w

N ^ '

N

średnia harmoniczna

średnia geometryczna

|

li':!:'

■

miarów wykonanych w każdej serii. Dla każdej z serii średniej arytmetycznej spełniony jest związek NkX& = więc znaleźć układ L równań:		zgodnie z definicją E^i xKj. Możemy
N\ii =	N, E^xbj • j—1
NiX2 =	n2 E ^x2ó ’ j=i	(3.1.9)
Nr.i,. =	E ^x,‘ó ■ i=i

Dodając do siebie stronami powyższe równania otrzymujemy:

W dalszym ciągu wykładu będziemy spotykali się z średnią arytmetyczną i średnią kwadratową.

Warunek (3.1.4) pozwala na jednoznaczne wyznaczenie wartości, wokół której grupują się wyniki pomiarów. Wyznaczone ze wzoru (3.1.7) wartości średnich arytmetycznych dla uprzednio podanych przykładowych serii pomiarowych wynoszą odpowiednio: 11.125 w przypadku 4 pomiarowi 11.000 w przypadku 5 pomiarów.

Zatem w celu znalezienia wartości, kolo której grupują się wyniki pomiarów, szukamy takiej wartości «, dla której suma kwadra.tów różnic z, -a jest najmniejsza. Poszukiwanie wartości, dla której jakieś wyrażenie ma wartość najmniejszą nazywa się minimalizacją. Przedstawiony sposób minimalizacji nosi nazwę metody najmniejszych kwadratów. Postępowanie polegające na wykorzystaniu warunku (3.1.4) w celu znalezienia wartości o na podstawie wyników pomiarów jest najprostszym przykładem zastosowania ■metody najmniejszych kwadratów. Do metody tej wrócimy w rozdziale 3.5 i rozdziale 5.

Wzór (3.1.8) pozwala nam obliczyć średnią arytmetyczną serii pomiarów zawierającej N wyników. Często zdarza się, że chcemy znaleźć wątłość średnią z różnych serii pomiarowych tej samej wielkości fizycznej x. Przypuśćmy. że. wielkość fizyczna. x była zmierzona w L seriach pomiarowych o jednakowej precyzji. Każda z serii pomiarowych miała inną średnią $k (k = 1,2, ...,£) i w każdej z serii wykonano inną liczbę pomiarów Znamy tylko £/<■ i Nk, nie znamy natomiast wyników poszczególnych po-

E Nk*k

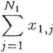
N₂    Ni.

E ^x*o + ■■■ + E ^x>'ó ■

i=i

(3.1.10)

.7 = 1