CCF20121001009

Twierdzenie 6 (Weierstrassa o osiąganiu kresów):

Jeśli funkcja f:(a,b)^>R w jest ciągła przedziale domkniętym (a,b), to jest w tym przedziale ograniczona

ie(a,4)    55

Twierdzenie 7. (Darboux): Dana jest funkcja ciągła

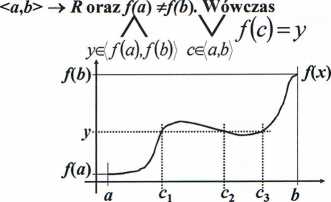
f(ci) = f(c₂) = f(ę₃) = y

Uwaga: Dla funkcji ściśle monofonicznej taki punkt c jest dokładnie jeden!    =6

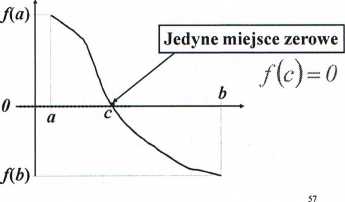
Wniosek: Dana jest funkcja ciągła i ściśle monofoniczna f:<a,b> —> R oraz zachodzi nierówność: f(a}f(b)<0. Wówczas istnieje dokładnie jedno jej miejsce zerowe.

f(aV(b)< 0