DSC00584

IMetenk środka masy korbowodu w przyjętym układzie współrzędnych, uwzględniając, EjśtóŚKyaa x(k jest jego płaszczyzną symetrii, na podstawie (18.4) wyznaczymy istotności (18,4):

I-

M

(18.12)

Masowy moment bezwładności korbowodu względem osi równoległej do osi otworów ido os Oy) i przechodzącej przez środek masy (18.12) przyjmie postać:

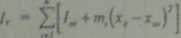
(18.13)

IŁ4.2. Metoda wahadła fizycznego lilii. Opis stanowiska pomiarowego

Korbowód zawieszony na sztywno zamocowanej pryzmie (rys. 18.7) wychylony z położenia itomowagi, wykonuje rucli drgający o okresie Tą. Znąjąc cechy geometryczne korbowodu i jego mg om mierząc okres Tą wyznaczymy masowy moment bezwładności korbowodu.

11.112. Metoda pomiaru

: Katbowód zawieszony w punkcie A (rys. 18.7) stanowi wahadło fizyczne o długości Mdtśtowsntj określmiej przez zależność (18.9). Wstawiając zależność (18.9) do (18.10) ^pufcizułcając otrzymamy następujące wyrażenie na masowy moment bezwładności wgłędem osi przechodzącej przez punkt zawieszenia A:

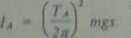
(18.14)

Ni podttswie tw. Steinera (18.7) moment bezwładności korbowodu względem osi pscbodzącaj przez środek ciężkości

/₍ • /» • ms •

(18.15)

Aby wyznaczyć moment bezwluduości /„ należy najpierw określić odległość s środka óętkośei C od punktu zawieszenia A W tym celu wyznaczamy moment bezwładności

mglętom Oli przechodzącej przez środek ciężkości dwa razy: ras wychodząc z olutsu wahań

7* prcy zawieszeniu w punkcie A, drugi ucz wychodząc z okresu wahań fi, przy zawieszeniu w punkcie fi Z porównania tych momentów otrzymamy:

_ glr\ - 4n‘l^l

^J " t(7i * Ti ) . fip7

Obłkając wartość s (18.16) wyznaczamy następnie Ją (18.14) oraz /<_• (1815).

(18.1*)

18.5. PRZEBIEG ĆWICZENIA

•    Wyznaczyć - ciężar korbowodu G [NJ (z dokładnością 0.03 N),

• odległość między punktami podwieszenia / /ni / (/ dokładnością 0.001 m)

•    Podwiesić korbo wód w punkcie A i wprawić go w ruch wulwdlpWy o kącie wahań mniejszym od I0*\ zmierzyć trzykrotnie czas 30 wahnięć. Należy zwrócić uwagę na to. aby osie otworów były równolegle do krawędzi pryzmy.

•    Zanotować wynik pomiaru w tablicy pomiarowej (tabela 18. i).

•    Powtórzyć czynności wymienione w punktach b i c podwieszając korbo wód w punkcia B.

•    Na podstawie zależności (18.16) wyznaczyć położenie środka masy, a następnie moment bezwładności korbowodu względem osi równoległej do osi otworów i proechodząpaj przez środek masy (IM. 15).

•    Wykonać szkic korbowodu, podzielić go na elementy składowe, zmierzyć oraz nanieść m nim te ich wymiary, które umożliwią wyznaczenie masowego momentu bezwładności korbowodu metodą analityczną. Wymiary te wpisać do tabeli 112,

•    Wyznaczyć metodą analityczną moment bezwładności kod>Qvyć^