image 5

Częstotliwość dolna f_dcl związana z pojemnością sprzęgającą C,

Schemat układu umożliwiającego wyznaczenie częstotliwości dolnej f_dC[ przedstawiono na rys. 4.7.

1

²"V.’

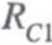
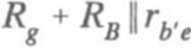
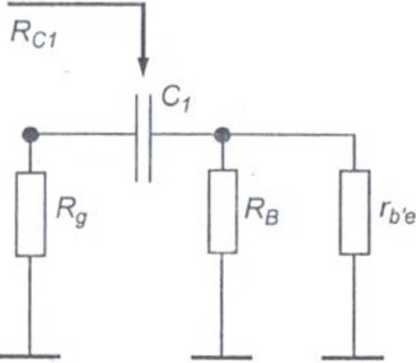
Rys. 4.7. Wyznaczenie f_dcx

1

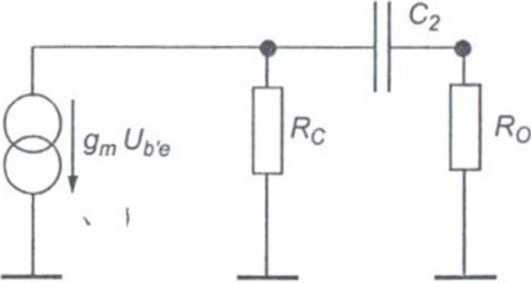
Rys. 4.8. Wyznaczenie f_dC2

Częstotliwość dolna f_dC2 związana z pojemnością sprzęgającą C₂

Schemat układu umożliwiającego wyznaczenie częstotliwości dolnej f_dcl

przedstawiono na rys. 4.8.

1

dC2

2 71

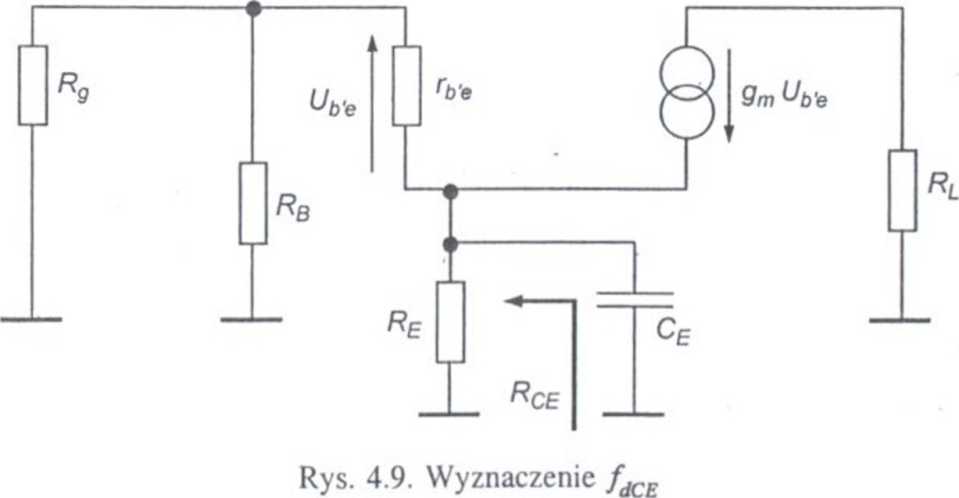
Częstotliwość dolna f_dCE związana z pojemnością C_E

Schemat układu umożliwiającego wyznaczenie częstotliwości dolnej f_dCE przedstawiono na rys. 4.9.

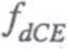
^rb'e ⁺

1

^ ⁿ ^CE^E

R_g\\R_B

^rb'_e ^{+ R}J^RB

Ku⁺¹

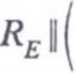
^h2U ^{+ 1}

OBLICZENIE GÓRNEJ CZĘSTOTLIWOŚCI GRANICZNEJ f

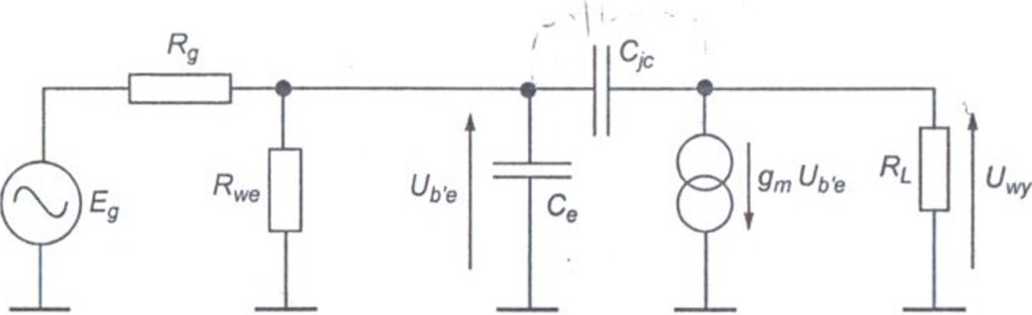
W schemacie zastępczym (rys. 4.5) uwzględnia się wszystkie reaktancje, przy czym reaktancje X_cl, X_c2, X_CE mają bardzo małą wartość i zastępowane są zwarciami. Tak zmodyfikowany schemat (rys. 4.10) posłuży do określenia górnej częstotliwości granicznej układu. Dominującą rolę odgrywają tu reaktancje pojemności tranzystora modelujące procesy gromadzenia ładunku w tranzystorze. Częstotliwość górną będziemy wyznaczać na podstawie sta-

Rys. 4.10. Schemat zastępczy dla zakresu dużych częstotliwości

łych czasowych, a nie transmitancji układu, gdyż jest to najprostszy i najłatwiejszy sposób. Ze względu na to, że wyznaczenie stałej czasowej na podstawie takiego schematu nie jest łatwe, postaramy się przekształcić pojemność. C_Jc. Skorzystamy z tzw. efektu Millera, w celu wyznaczenia takich pojemności C_m dołączonej do wejścia i C_m dołączonej do wyjścia, które są równoważne pojemności C_jc. Mamy więc:

^Cm = (! ⁺8M^Cjc ^a 8_mR_LC_jc

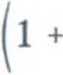
1

8_m^RL

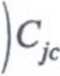
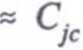
Ponieważ C_m ~ C_jc (a C_jc jest bardzo mała), drugi biegun charakterystyki wprowadzany przez C_m będzie leżał znacznie wyżej niż pierwszy wprowadzany przez C_W1 i C_e od strony wejścia. Dlatego też nie będziemy zajmować się wpływem drugiego bieguna i pominiemy w schemacie C_m (patrz rys. 4.11).

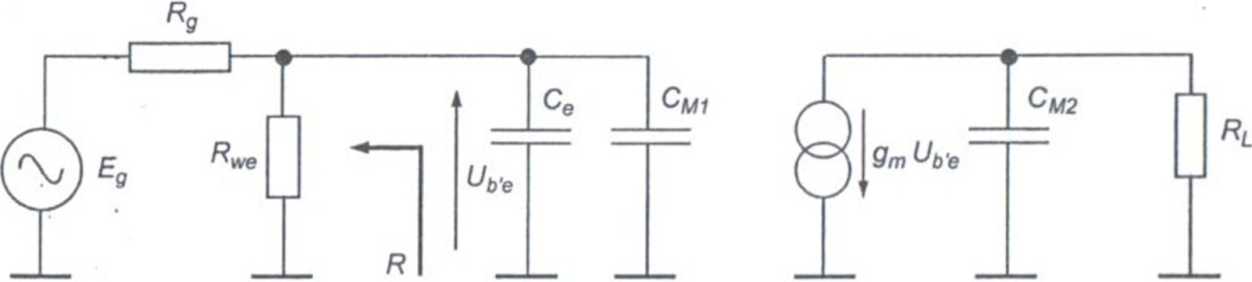
Rys. 4.11. Schemat układu po zamianie pojemności C^ na C_M1 i

69