IMGh92

228

Pola komutacyjne przestrzenno-czasowe z komutacja kanałów

02J13C7J. ze dyskutowane własności danego pola komutacyjnego są niezależne od lego. czy struktura jest regularna, czy zmodyfikowana.

Sformułujemy i udowodnimy następujące twierdzenie dotyczące pola 1. rys. 7/21.

Twierdzenie 7.1 [14], Pole komutacyjne TS/3/FW zbudowane z komutatorów pnesirzennn-czasnwych jest nirhtnknwotnr w wąskim sensie wtedy i tylko wtedy, gdy

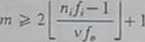
(7/8)

Dowód: Będziemy rozpatrywać tylko jedna ..połówkę" pola cztcroprzc-wodowego. Warunek konieczny udowodnimy przez podanie takiego ciągu zgłoszeń, który spowoduje zajęcie m = 2L(n./,— l)/(v/„)J+ I komutatorów sekcji środkowej. Do wyboru dróg połączeniowych będziemy stosować zmodyfikowany algorytm quasi-przypadkowy. Założenie to nie wpływa na ogólność rozważań, ponieważ dowodzimy nieblokowalności w wąskim sensie, czyli dla każdego algorytmu wyboru dróg połączeniowych. Modyfikacja algorytmu quasi-przypadkowego (patrz p. 6.5) będzie polegała na tym. ze przy zestawianiu dróg połączeniowych prowadzących między tymi samymi komutatorami sekcji pierwszej i trzeciej będą zajmowane kolejno wszystkie wolne kanały do wybranego komutatora sekcji środkowej, następnie wszystkie wolne kanały prowadzące do kolejnego komutatora itd. Gdy natomiast kolejne zgłoszenie pojawi się na innym komutatorze sekcji pierwszej, droga połączeniowa będzie zestawianą przez wolny komutator sekcji środkowej, następujący po zajmowanym ostatnio. Symbol (a.b) będzie oznaczać połączenie między komutatorem a sekcji pierwszej i komutatorem /> sekcji trzeciej.

Krok I. Zestaw    1 )/(''/jJ połączeń (x.y). x * y. Połączenia te będą

przechodziły przez    1)/(‘7»)J różnych komutatorów

Krok 2. Zestaw v/,L(n,/, - 1 )/(v/,)J połączeń (y.-O- Połączenia te będą przechodziły przez [("Ji-U/WJj następnych komutatorów sekcji środkowej Zestawienie połączenia (jt.jO wymaga użycia komutatora o numerze 2L(h,/,- U/(‘7„)J + 1. co kończy dowód warunku koniecznego.

Warunek dostateczny udowodnimy, rozpatrując najbardziej niekorzystny stan pola komutacyjnego przedstawiony na rys 7/36. podobnie jak to zrobiliśmy w’ dowodzie twierdzenia 6.1. W stanie tym zajętych jest n,/, — I kanałów wejściowych w wybranym komutatorze sekcji pierwszej oraz u,/, - I kanałów wyjściowych w wybranym komutatorze sekcji trzeciej. Nic istnieją przy tym żadne drogi połączeniowe między wybranymi komutatorami sekcji zewnętrznych Kanały między pierwszą a drugą sekcją są zajmowane kolejno, czyli wybieramy

Mcblakownlność i przaslrnjnlność pól pwslnnnnocznsowyrh

229

n,--1

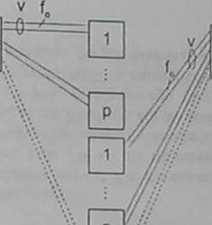
P

f,

n.

m

Rys. 7/36 Najbardziej niekorzystny stan pola trzysekcyjnego

najpierw wszystkie kanały prowadzące do pierwszego komutatora sekcji środkowej, następnie kanały prowadzące do komutatora drugiego itd. Ostatecznie zajmujemy n,/,—1 kanałów w traktach micdzysckcyjnych. Wynika stad. ze w vp = [(n,/ -    traktach prowadzących z wybranego

komutatora sekcji pierwszej nie ma już wolnych kanałów. Jeżeli (n,/,— 1 )/(v/„) nie jest liczba całkowita, to istnieją wolne kanały, prowadzące do ostatniego zajmowanego komutatora. Podobnie zajmujemy kanały w traktach między druga a trzecia sekcja. W tym przypadku rozpoczynamy zajmowanie kanałów od pierwszego całkowicie wolnego komutatora sekcji środkowej. Jeżeli    (nj, — 1)/(»/.)    me jest liczba całkowita, to

I-L(n;/,-D/(v/,)J|i7„ kanałów laczynn przez częściowo zajęty komutator sekcji środkowej.

Można zauważyć, ze przy i- =/,=/„= I otrzymujemy warunek m 5 2zt| — I. czyli powyższe twierdzenie jest uogólnieniem twierdzenia Ciosa.

Podamy obecnie, bez dowodów, warunki nieblokowalności trzech innych typów- pól zbudowanych z komutatorów przestrzenno-czasowych |I3. 16).

Przypuśćmy, że należ)' zestawić połączenie miedz- wolnym kanałem wejściowym wybranego komutatora sekcji pierwszej a wolnym kanałem wyjściowym wybranego komutatora sekcji trzeciej. Jeżeli (u,/, — l)/(i'/.) niejesi liczba całkowitą, połączenie to może być zestawione przez częściowo zajęty komutator sekcji środkowej. Jeżeli natomiasi liczba (n,f- I )J(vf,)jcsi całkowita, połączenie między rozważanymi kanałami wymaga dodatkowego, wolnego komutatora. W obu przypadkach należy użyć m = 2p+1 komutatorów-. Kończy to dowód warunku dostatecznego.