IMGh91

„ormitacyjne przestrzenno-czasowe z komutacją kanałów    226

Oanc weisoowe    Ą P¹ / Cl A Ol x ( a; \ q₂ ^

2npisywanie do PO (    ' ( Al ^ < Bi ) ( Cl j (    (    "\ ( A2^j' (

Odczytywanie z PO _ O _____$    Q (i)

Oanowyjśoowo (.. TA _ IX.®? .X.. ^AJ_X (    _X_    ~ Y ■

Rys. 7/34 Przykładowy przebieg czasowy dla komutatora z pojedynczą pamięcią danych utrzymana. ponieważ szczeliny wyjściowe zawierają dane pochodzące z. dwu różnych ramek wejściowych.

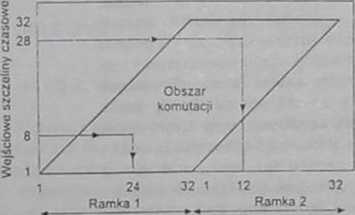
Opisane zjawisko ntoz.c hyc' objaśnione prz.y użyciu rys. 7/35a. Założyliśmy tu. ze trakty wejściowy i wyjściowy zawierają po 32 szczeliny czasowe. Przykładowe połączenie szczeliny wejściowej 8 ze szczeliną wyjściową 24 jest uzyskiwane w ramach tej samej ramki Jednakże, gdy zawartość szczeliny wejściowej 28 chcemy przesiać do szczeliny wyjściowej 12. następuje opóźnienie o jedną ramkę. Problem ten nasila się w przypadku pól wielosekcyjnych. np.

a)

Wyjściowe szczeliny czasowe

b)

		Obszar
		komutaqr
		T

32 t

Ramka I

12    24

Ramka 2

32

S 32 0 28 >»

O

N

O

a

0

1    8

O

v»

O

5 i

Wyjściowe szczeliny czasowe

Rys. 7/35 Funkcje przejścia komutatorów czasowych, a) komutator z poiedynczą pamięcią danych, b) komutator z podwójną pamięcią danych

Nieblokowalność, przestrajalność pól przesirzenno-czasowycb    ₂₂₇

i o t isrs^{h cMsowyeh} ***^www^ •**? —.....—

Jednym zc sposobów utrzymania integralności połączenia wieloszczclino-wegojest uzycc komutatorów czasowych z podwójna pamięci.,. ,nk„ !, jak ten t. rys. 7/4. W przypadku takiego komutatora nic występują przesunięcia ramek, lak jak to pokazano na rys. 7/35b. Integralność można także zapewnić przez zastosowanie odpowiedniego algorytmu sterowania w konwencjonalnym komutatorze czasowym (29]

7.6

nieblokowalność i przestrajalność pól przestrzenno-czasowych

Znaczenie struktur pól komutacyjnych, w których me występują straty zgłoszeń na skutek blokady wewnętrznej, rośnie zc względu na wymagania transmisji danych, a także z powodu znacznego zwiększenia szybkości komutowanych strumieni (np. w systemach SDH). Określenie warunków meblokowalności i przestrajalności w przypadku pól przeslrzenno-czasowych z rozdzielonymi sekcjami czasowymi i przestrzennymi jest stosunkowo proste. Wystarczy przeanalizować odpowiednie ekwiwalenty przestrzenne metodami omówionymi w rozdziale 6. Na przykład łatwo zauważyć, że pole typu T-S-T z rys. 7/14 jest. na mocy twierdzenia Ciosa, nicblokowalne w wąskim sensie, gdy krotność traktu międzysekcyjnego spełnia warunek m $ 2n— 1.

Problem staje się bardziej złożony przy rozpatrywaniu pól zbudowanych z jednorodnych komutatorów przestrzenno-czasowych. Ekwiwalenty przestrzenne takich pól odpowiadają słabiej zbadanym polom niezupełnym W celu uproszczenia zapisu różnorodnych struktur pól zbudowanych z komutatorów przeslrzenno-czasowych zaproponujemy następującą notację. Pole komutacyjne będzie oznaczone przez zbiór pięciu lub mniej symboli: AIBICIDIE. przy czym ,4 opisuje rodzaj pola komutacyjnego. B jest liczbą sekcji, C określa metodę zapewniania transmisji dwukierunkowej. D oznacza własności kombmatoryczne. a E strukturę regularną bądZ zmodyfikowaną. Pozycji A mogą odpowiadać następujące symbole:

OS. L — pole jednostronne z połączeniami pędowymi, (ang. one-sidid. loops): OS, T _ pole jednostronne z komutatorów trójkątnych, (ang. one-sided.

iriangidar)-,

TS — pole dwustronne (ang. two-sided).

W miejscu symbolu C będziemy używać FW dla oznaczenia pola cztero-przewodowego (ang. four-w.rc). bądź W - dla oznaczenia pola dwuprzewodowego (ang. mo-w/re). Własności kombinatoryczne będą oznaczane przez. B w przypadku pola blokowalncgo (ang. błock,n_S). NB dla pola "'^lokowalnc,

(ang. non-bloi. ' g)    nrzcz REG a zmody fikowane'przcz^? MOD.

Struktury rcculumc oznaczymy przez RbO,    j    . «

ST «“U>li «.|» V PO-!™- » P*"- “