matma21

Zastosowania matematyki w ekonomii

Zadanie 1.9. Fabryka czekolady produkuje 3 rodzaje czekolad: deserową, mleczną i z orzechami. Do produkcji każdej z nich wykorzystuje 3 składniki: miazgę kakaową, cukier i mleko w proszku, których obecne zasoby w magazynie są ograniczone do ilości odpowiednio 209, 128 i 46 jednostek. Ilości składników potrzebnych do wyprodukowania jednej jednostki każdej czekolady przedstawione zostały w poniższej tablicy:

Zadanie 1.10. Rozwiązać układy równań metodą eliminacji Gaussa:

(2x₁ + x₂

x₁ + 2x₃ = 1 x₂ + 3x₃ = -2

b)

2x₁ — x₂ = 1 —x₁ + x₂ = 2

,    .    -    *3 = J-

c) x_a + 2x₃ = 2 (,3x₁ + x₂ + x₃ = 3

1x_x — 2x₂ — x₃ + 3x₄ = 5 2x_t — 4x₂ - 2x₃ + 6x₄ = 10 2x_x + x₂ + x₄ = 20

'2x₁ + 3x₂ — x₃ = 1 3x_x - 2x₂ + 3x₃ — 0 x_x + 3x₂ + 2x₃ = 5 ,3x_x + 2x₂ + 2x₃ = 3

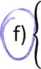
—2x_x + 3x₂ — x₃ = 0 x_x + 2x₂ + x₃ = 2 X\ ~ 5x₂ = 3

Rodzaj czekolady

Surowiec	deserowa	mleczna	orzechowa
miazga kakaowa	9	7	7
cukier	5	4	6
mleko w proszku	0	3	2

Ile jednostek każdego typu czekolady należałoby wyprodukować, aby zużyć bez reszty cały zapas surowców w magazynie?

Zadanie 1.11. Rozwiązać układy równań korzystając z wzorów Cramera:

6

5

-1

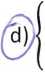
Xi + x₂ + x₃ = 0 2x_x + 3x₂ + 2x₃ = 0 x_x — 2x₂ + 2x₃ = 1

( Xi - x₂ + 2x₃ =2    ,    ,    „    r2xi + x₂ + 3x₃ =

a) -Xi + x₃ = -4 b) Z¹, ₂!² 15 c)j Xi + 3x₂ + x₃ = (2x4 - x₂ + 3x₃ =0    ^1    2    (    x₂-x₃ =

Zadanie 1.12. Za pomocą operacji elementarnych znaleźć macierze odwrotne do macierzy A-H z Zadanie 1.8 oraz do macierzy:

1    -0,2    -0,4-

-0,1    0,3    -0,2

0,2    -0,3    0,2.

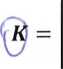
Zadanie 1.13. Wyznaczyć macierze odwrotne do podanych wyżej stosując metodę wyznacznikową (za pomocą dopełnień algebraicznych).

Zadanie 1.14. Stosując macierze odwrotne rozwiązać układy równań z Zadanie 1.10 b), f), Zadanie 1.11 a) oraz

równania: 4    2

-1 3

X =

8 6 5 -5

b)x[

2

L2

Zadanie 1.15. Obliczyć wyznacznik macierzy C = [SB+fAB^J^AjB'¹, jeżeli macierze A i B są nieosobliwymi macierzami stopnia n.

Zadanie 1.16. Rozwiązać równania (wyznaczyć macierz X): a) AXA^-1 = B    b) B ^ŁXA^T = I    c) (A^_1)^T+A = BX(A^T)'¹.

str. 2