matematyka05
Matematyka 1 OO
Zastosowanie twierdzenia Pitagorasa w zadaniach (1)
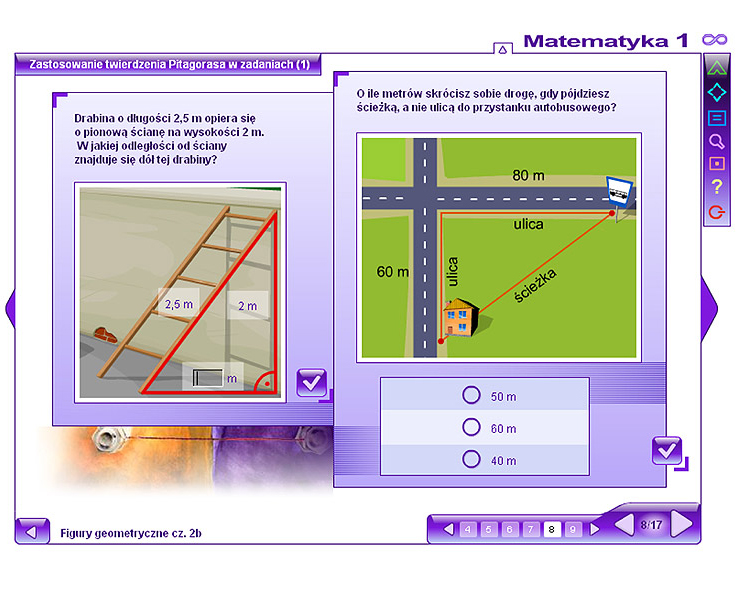
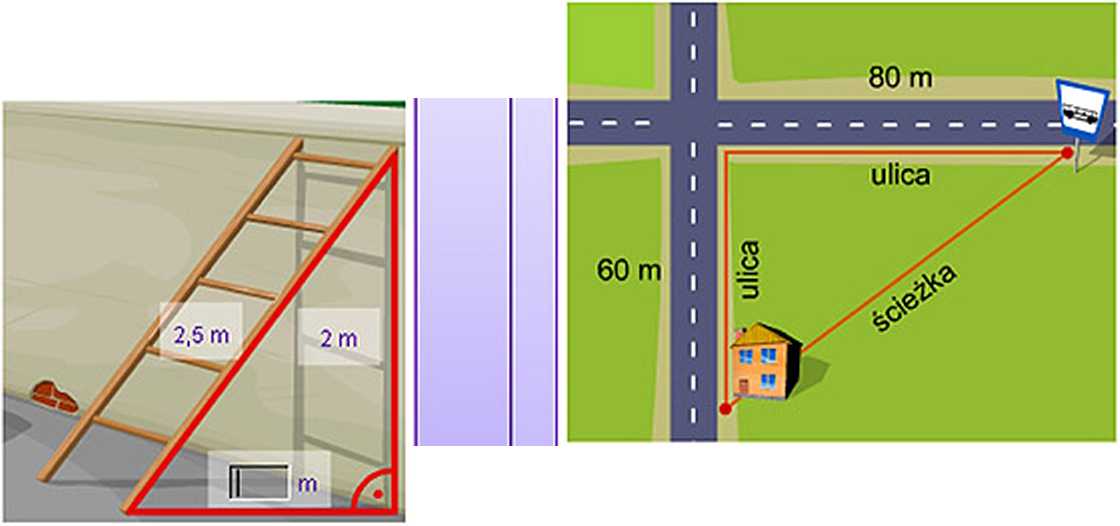
O ile metrów skrócisz sobie drogę, gdy pójdziesz ścieżko, a nie ulico do przystanku autobusowego?
Drobina o długości 2,5 m opiera się o pionowo ścianę tra wysokości 2 itr. W jakiej odległości od ściany znajduje się dół tej drabiny?
Figury geometryczne cz. 2I>
prrnrr~nTT
Wyszukiwarka
Podobne podstrony:
ScanImage002 Obliczanie ryzyka z zastosowaniem twierdzenia Bayesa Zadanie 1. Choroba Huntingtona jes
54 (102) 54 [ TRÓJKĄTY PROSTOKĄTNE3 Zastosowania twierdzenia Pitagorasa 12. Oblicz długość przekątne
2.2. Zastosowania twierdzenia Pitagorasa Przyjmujemy, że y/l = 1,41, i obliczamy c = 70 • 1,41 = 98,
CCF20141113�000 Zastosowania matematyki w ekonomii 2. Funkcje jednej zmiennej Zadanie 2.1. Pani Krys
Nie tylko przed sprawdzianem • Matematyka Zadanie 8. O ile mniej kosztuje jeden kilogram karmy w opa
Temat: Twierdzenie Pitagorasa. Twierdzenie Pitagorasa jest jednym z najważniejszych twierdzeń matema
Matematyka III Sprawziany dla Gimnazjum�16 • obliczyć długość odcinka w ostro stupie, korzystając
img015 (50) Egzamin z matematyki termin I (ZIP semestr letni) Zadanicl .Wyznaczyć — J (ci dx Zadanie
img027 Egzamin z matematyki dla I roku IMIR Każde zadanie punktowane jest w skali 0-20 punktów. Egza
stat Page) resize 29 Statystyka matematyczna Co istotne w twierdzeniu 3.11, dwie trochę tylko inacz
Kangurek 2008 zadania 011 jjr Matematyka z wesołym Kangurek - test III V Zadania po 3 punkty 1. &nbs
Kangurek 2008 zadania 020 Matematyka z wesołym Kangurkiem Matematyka z wesołym Kangurkiem Kangurek -
skanuj0092 Praca wakacyjna na egzamin poprawkowy z matematyki - Id. I GM Rozwiąż poniższe zadania w
egzamin matematyka2 Zestaw 1 i/a) Podać twierdzenia określające warunki wystarczające dla różniczkow
egzamin matematyka 00Zestaw 7 a) Podać twierdzenia Abela o zbieżności całki Jf(x)g(x)dx i o a ■• zbi
egzamin z matematyki zestaw 3 Egzamin z Matematyki (25 czerwiec 2010) Zestaw 3 Zadanie 1 3 równania
więcej podobnych podstron