Matematyka III Sprawziany dla Gimnazjum16

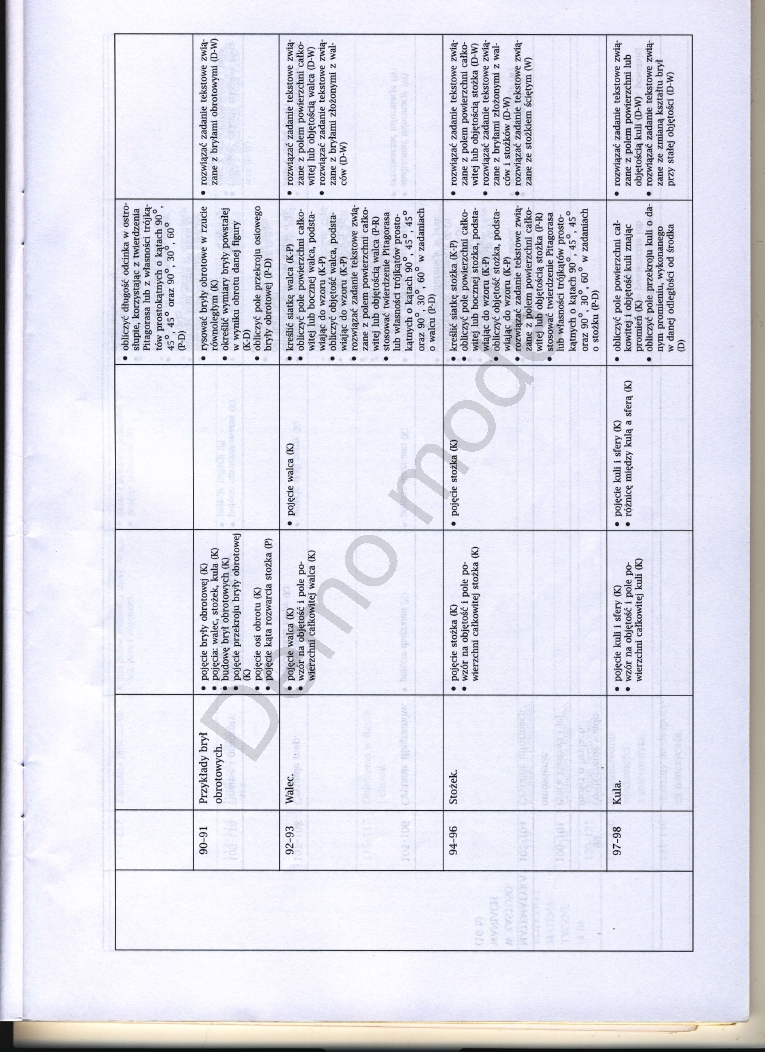
					• obliczyć długość odcinka w ostro stupie, korzystając z twierdzenia Pitagorasa lub z własności trójkątów prostokątnych o kątach 90°. 4S°, 43° oraz 90°. 30°. 60° (PD)
	90-91	Przykłady brył obrotowych.	•    pojęcie bryty obrotowej (K) •    pojęcia; walec, stożek, kula (K) •    budowę bryt obrotowych (KJ •    pojęcie przekroju bryty obrotowej 00 •    pojęcie osi obrotu (K) •    pojęcie kąta rozwarcia stożka (P)		•    rysować bryty obrotowe w rzucie równoległym (K) •    określić wymiary bryty powstałej w wyniku obrotu danej figury (K-D) •    obliczyć pole przekroju osiowego bryty obrotowej (P-D)	• rozwiązać zadanie tekstowe związane z bryłami obrotowymi (D-W)
	92-93	Walec.	•    pojęcie walca (K> •    wzór na objętość i pole powierzchni całkowitej walca (Ki °o	• pojęcie walca (K) /v	•    kreślić siatkę walca (K-P) •    obliczyć pole powierzchni całkowitej lub boczne) walca, podstawiając do wzoru (K-P) •    obliczyć objętość walca, podsta wiąjąc do wzoru (K-P) •    rozwiązać zadanie tekstowe związane z polem powierzchni całkowitej lub objętością walca (P-R) •    stosować twierdzenie Pitagorasa lub własności trójkątów prostokątnych o kątach 90°, 43°, 4S°	•    rozwiązać zadanie tekstowe związane z polem powierzchni całkowitej lub objętością walca (D-W) •    rozwiązać zadanie tekstowe związane z bryłami złożonymi z walców (D-W)
					oraz 90°, 30°, 60° w zadaniach o walcu (P-D)
	94-96	Stożek.	•    pojęcie stożka (K) •    wzór na objętość 1 pole powierzchni całkowitej stożka (K)	• pojęcie stożka (K)	•    kreślić siatkę stożka (K P) •    obliczyć pole powierzchni całkowitej lub bocznej stożka, podstawiając do wzoru (K-P) •    obliczyć objętość stożka, podstawiając do wzoru (K-P) •    rozwiązać zadanie tekstowe zwią zane z polem powierzchni całko-	•    rozwiązać zadanie tekstowe związane z polem powierzchni całkowitej lub objętością stożka (D-W) •    rozwiązać zadanie tekstowe związane z bryłami złożonymi z walców i stożków (D-W) •    rozwiązać zadanie tekstowe związane ze stożkiem ściętym (W)
					witej lub objętością stożka (P-R) • stosować twierdzenie Pitagorasa lub własności trójkątów prostokątnych o kątach 90°. 45°. 45° oraz 90°. 30°. 60° w zadaniach o stożku (P-D)
	97-98	Kula.	•    pojęcie kuli 1 sfery (K) •    wzór na objętość 1 pole powierzchni całkowitej kuli (K)	•    pojęcie kuli 1 sfery <Kł •    różnicę między kulą a sferą <K)	•    obliczyć pole powierzchni całkowitej i objętość kuli znając promień (K) •    obliczyć pole przekroju kuli o danym promieniu, wykonanego w danej odległości od środka (D)	•    rozwiązać zadanie tekstowe związane z polem powierzchni lub objętością kuli (D-W) •    rozwiązać zadanie tekstowe związane ze zmianą kształtu brył przy stałej objętości (D-W)