P3230318

^fproi®yina^a^fe3ni5Rwa3raJów^ Aproksymacja jednostajna Równania nietniowel

Metoda bisekcji (połowienia)

Założenie: f: [a, b] -> R, f e C[a, b], f{a)f(b) < 0, tj. f zmienia znak w [a, b]. Z tych założeń (własność Darboux) wynika, że w (a, b) f ma zero i metoda bisekcji korzysta z tej własności.

03 a bi

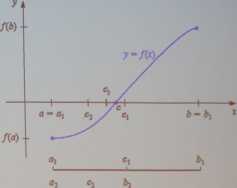
Rysunek 2: Metoda bisekcji

Jeśli f{a)f(b) < 0, to obliczamy Ci = (a + b)/2 i sprawdzamy, czy f(a)f(Ci) < 0. Jeśli tak, to f ma zero w [a,q] i kładziemy ai/= a, b\ = Ci. W przeciwnym razie zero jest w [ci, b] i kładziemy a! = c_t, b₁ = b. Nowy przedział jest dwa razy krótszy niż poprzedni i zawiera zero f i postępowanie to można powtórzyć.

©Zbigniew Bartoszewski (Politechnika Gdańska) METODY NUMERYCZNE    43/«B