3582360665

Układ równań

r nx + (n + l)y - n + 2 ((/» + 3)x + (n + 4 )y u + 5 Metoda Cramera Wyznacznik qłówny ty * 0

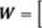
n    /i + 11

n + 3 n + 4J

= n(n + 4) - (n + 3)(n + 1) =

= u² + 4n - n² — n — 3/i — 3 = —3

Wyznaczniki porządkowe

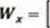
fu + 2    11 + 1 ]

In + 5 11 + 4]

= (n + 2)(n + 4) - (n + 5)(n + 1) = n² + 4n + 2n + 8 - n² - n — 5n - 5    3

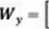
11    11 + 2 ]

ii + 3 11 + 5l

- n(n + 5) - (n + 3)(n + 2) -= ir + 5n - /t² - 2/i - 3/j - 6 = -6

— 1 Odpowiedź:    (x =* — 1

(y-2

W, _3_ _

~ T7 ⁼ -3 ~

x