gaussssru Kopia

Metoda eliminacji wspaniałego! Gaussa Metoda eliminacji Gaussa pozwala nam obliczyć układ n równań z n niewiadomymi Ax=b. Przekształcamy w niej macierz współczynników A do macierzy trójkątnej górnej R, z której następnie obliczamy ostateczne rozwiązanie - czyli wektor x. Macierz trójkątną górną R otrzymujemy w następujący sposób: (Przez macierz (A,b) rozumieć będziemy macierz współczynników A z dodaną na końcu kolumną wyrazów wolnych b)

1.    >W macierzy (A,b) szukamy elementu a_ri różnego od zera i przechodzimy do następnego punktu. Jeżeli natomiast nie istnieje taki element

to znaczy, że macierz jest osobliwa i nie możemy rozwiązać tego układu.

2.    ► Zamieniamy wiersz r-ty i pierwszy.

3.    ► Odejmujemy od i-tego wiersza macierzy lj krotność wiersza i-tego i pierwszego. Można to przedstawić za pomocą wzorów: (i=2,3,...,n j=2,3,...,n) _Q;: = q_;; — l_{r a}

*ż,    *ij 1 i

b=b-l_r

b,

^an

gdzie 1= —

a

u

4. ► Następnie wywołujemy tą procedurę od punktu pierwszego rekurncyjnie dla macierzy (A',b')

- czyli macierz (A,b) pomniejszoną o pierwszą kolumnę i pierwszy wiersz.

(A, b) =

a

a-

a.

11	^an	... aln	K
21	*22	... Oto	^b2
n\	**2	... am	^bn

^a22    - ^a2n ^b2

QrH ...    b,

rm n

Przykład, niech będzie dana macierz A oraz wektor b, z których tworzymy macierz (A,b)

	3	1	0	-3
(A, b) =	1	2	-1	0
	0	-1	3	0
po przekształceniach:
	3	1	0	-3
	0	5 3	-1	1
	0	-1	3	0

natępnie wywołujemy procedurę rekurencyjnie dla:

5 3	-1 1
-1	3 0

po przekształceniach:

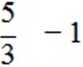
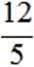
Ponieważ ostatniej macierzy nie możemy już rekurencyjnie wywołać (po odcięciu górnego wiersza i prawej kolumny zostanie wektor), zatem otrzymaliśmy szukaną macierz R i wektor c, z których wyznaczamy ostateczne rozwiązanie

	3	1	0	-3
(R, c) =	0	5 3	-1	1
	0	0	12 y	3 5

x[3]=0.25 x[2]=0.75 x[1]=-1.25

Wybór częściowy elementu podstawowego uzyskamy wybierając za element, a w punkcie pierwszym |a_r1|=max|a_h| i=1,2,...,n

Pełny wybór elementu podstawowego poprzez |a_rs|=max|aij| j=l,2,...,nj=1,2,...,n Musimy przestawić wiersz r-ty i pierwszy oraz kolumnę s-tą i pierwszą (zmiany kolumn należy zapamiętać gdyż powoduje ona zamianę niewiad Gdy przekształcimy już macierz współczynników A do macierzy trójkątnej górnej R, oraz wektor b do wektora c możemy już wyznaczyć ostateczne rozwiązanie ze wzoru: (i=n,n-1,...,1)

n

^cr X ^r^^k

k = i+ 1