scan'

{y = 4    równanie kwadratowe rozwiązu-

z = 8 — x    jemy posługując się wzorami

x² - 8jc +16 = 0    A = b²- Aac

_    _-b + 'lA

^1_ 2a ^,Xl~    2a

a = l, b = -6, c = 16

A = (-8)² - 4-1-16 = 64 - 64 =0

X

1,2 ^_

Z*>₌^z8i₌J_₌₄

2 a 2 1    2

lub

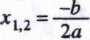
fy = 4 z=8-x [ jc = 4

fy = 4

i z = 8 - 4    w miejsce x podstawiamy znalezioną

[ x = 4    wartość

(y = 4 - z = 4 x = 4

Odp. Liczby te, to: 4, 4, 4.

Zad.11.

Między liczby 5 i 45 wstaw liczbę x tak, by liczby 5,x, 45 tworzyły ciąg geometryczny.

Rozwiązanie:

Liczby 5,*, 45 tworzą ciąg geometryczny, gdy

x =5-45    wynika to z uwagi

czyli    ze strony

x² = 225

stąd

x = -15	lub	II H-*
Odp. x = -15	lub	x= 15

Zad.l2.

Dane są cztery liczby. Trzy pierwsze z nich tworzą ciąg geometryczny, zaś trzy ostatnie ciąg arytmetyczny.

Suma liczb skrajnych równa się 14, suma środkowych równa się 12. Znajdź te liczby.

Rozwiązanie:

Oznaczamy szukane liczby przez x,y,z,i.

Każde zdanie z treści zadania przetwarzamy na równanie.

y²-x-z z-y= t- z

x + t = 14 y + z = 12

<— Trzy pierwsze z nich tworzą ciąg geometryczny (równość wynika z ^ ze strony 5&.) <— trzy ostatnie tworzą ciąg arytmetyczny (równość wynika z definicji ciągu arytmetycznego)

<— suma liczb skrajnych równa się 14 «— suma liczb środkowych równa się 12

Powstał układ równań, który należy rozwiązać .

' y² = x -z 2 z = y+ t 1 x + t = 14

, y + ^ = 12 y=*-z

2 z = y + ł t=U-x

_<z=U-y

równanie powstało z przekształcenia

z-y = t- z z-y-t+ z = 0 2z - y - t = 0 2 z = y + t

i— z równania x + t = 14 obliczamy t <r- z równania y + z = 14 obliczamy z

y² = x ■ (12-y)    <— w miejsce z podstawiamy 12-y

2(12 -y) = y + (14-*)    <— w miejsce f podstawiamy 14 - *

r = 14 —jc

_wz= 12-y

' y²= \2x-xy I 24 - 2y = y + 14 - x 1 r = 14 - x

„ z ⁼ 12 — y

57