scan5

Ad c

czyli

Ad d

czyli

lim u_n - lim (a„ • b_n) = lim^ a_n ■ lim b_n lim u_n = 6

lim v„ = lim (a_n: b_n) = lyn a_n : lim b_n

= 2-3 = 6

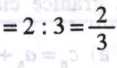
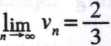
₍ _ n~ + 3n — 2 1 + 2 + 3 + ... + n

Zad.21.

Znajdź granicę

Rozwiązanie:    _n(n+V)

Skorzystamy ze wzoru 1 + 2 + 3 + ... + n =—^udowodnionego w rozdziale dotyczącym indukcji matematycznej.

Zamiast sumy 1 + 2 + 3 +... + n wpisujemy ⁿ

,    n^z + 3n-2    n^z + 3n-2    n^z + 3n-2

■MSL i ₊ 2 + 3 +... + « “M    “i™    + »

— lim

n —

n^z + n

._oo

/ / /

2«² + 6n - 4

-4

n² + n

1 i

= (— } =

* no '

1 +J-

z²/⁰/

2 + -*-4

I i

i o

Zad.22.

4 n³ + n² - 1

Znajdź granicę

Rozwiązanie:

wykonujemy zaznaczone w liczniku działania

(n²-9)(l-n)    >. n¹ -n³-9 + 9n .

" ™ 4n³ + n² - 1    " ^    4n³ + nr - 1

= lim

ĄV

-n³ + n² + 9n -9

4n³ + n² -1

i i 1

OO    OO —1

/-¹/⁰ // -l⁺7 ⁺ ^-^    (-1,

• lun---:-:--(-t-|

~    4+——-r    4

~jŁ j. «i . 9n _ 9_

^    ^    «3 _n3

4«3    _«2    _ J_

_b3 T „3    .3

4

i

Zad.23.

Znajdź granicę a_n =

3n + 1 n + 2

Rozwiązanie:

Najpierw znajdujemy granicę

3 n + 1 n + 2

a potem otrzymaną

liczbę podniesiemy do potęgi piątej. Tak można zrobić, ponieważ wykładnik potęgi nie zależy od n, jest liczbą.

i    /    /°

'    i/¹    J?+2.    /+±^/ i

lim — {~ 1 ⁼ lim ~—T ⁼ lim ~—t = {■Ą~ I = 3

n+2

i I

oo 2

n —+00 i A n -

1 + -Ł

"

4 i 1 0

1

Teraz podnosimy uzyskaną liczbę do potęgi 5, uzyskując 3⁵ = 243 Odp. W a_n = 243

73