Skrypt)

II. Obliczanie pochodnych.

Twierdzenie 3.1 (o różniczkowaniu działań arytmetycznych) Jeżeli funkcje f i g są różniczko-

* f

w Ginę w punkcie x to również funkcje f zzg, f ■ g, — są różniczkowalne w punkcie x. Ponadto: (/ = g) 00 = f i:i)-g'(x)

f

(a ■ /) (x) = a ■ f(x) gdzie a s IR

j.

(f ■ g) W = /'CO • g(0 - /O) • g'(0

(x)

vrzos dodatkowym założeniu

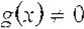
g²(x)

Twierdzenie 3.2 (o różniczkowaniu funkcji odwrotnej) Jeżeli funkcja f jest ciągła i monofoniczna w przedziale U i różniczkowalna w pewnym punkcie x,, s U, to funkcja do niej odwrotna

y —jest różniczkowalna w punkcie y₀ = /(x₅) a, ponadio:

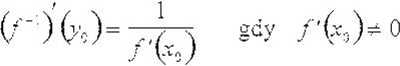
Twierdzenie 3.3 (o różniczkowaniu funkcji złożonej). Jeżeli funkcja f jest różniczkowalna w punkcie x| i hinkcja g jest różniczkowalna w punkcie y₀=/{x₃)i to funkcja złożona x > (g = /)x) = g(f{x)) jest różniczkowalna w punkcie xę, a ponadto zachodzi związek:

(§ *'/) fe) = /'(g(w)) -8'IW

Poniższe zadania pokazuj aj ak w praktyce posługiwać się tablica, pochodnych i Twierdzeniami 3.1, 3.2, 3.3. We wszystkich zadaniach naieży wyznaczyć pochodną funkcji / dlatego ograniczymy sie :v!ko do podania funkcji.

Zadanie 3.7

f(x)' = X" + COSX -r COS ~ '    v2

Zadanie 3.9

f(x) = 3x^> - sin* - 5*

Zadanie 3.10

/CO = .0 • cos*

Zadanie 3.11

/(*) = :rV

/'CO = 4*^J - sin*

/'(*) = 15x^J - cos* - ki5 • 5^X

/'(*) = 2xcosx + x" (— sinx) = x(2cosx - xsinx)

/'(*) = 3x“td + x'e^x - *V'(* -r 3)