wielokaty ko≥a i okrÍgi A`

GRUPA A"

WIELOKńĄTY, KOŇĀA I OKRńėGI
1. W kaŇľdym r√≥wnolegŇāoboku ABCI>.
A. AC JL DB C. \AD\ = \DB\
B. \AC\ = \DB\ D. \AO\ = \OC\
2. Pole kola o promieniu r wyraŇľa sińô wzorem: A. 2rrr B. rrr2 C. 2rrr2 D. nr
3. Tr√≥jkńÖt prostokńÖtny ma przyprostokńÖtne x i y oraz przeciwprostokńÖtnńÖ z. Z twierdzenia Pitagorasa wynika r√≥wnoŇõńá:
A. x2 + y2 = z2 B. x2 + z2 = y2
C. x + y = z D. y2 + z2 = x2
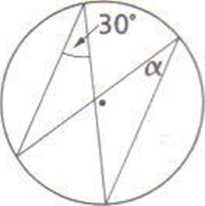
4. Zaznaczony kńÖt ma miarńô:
A. 60¬į C. 30¬į
B. 15¬į D. 180¬į
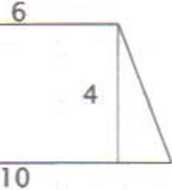
5. Jakie pole ma trapez przedstawiony na rysunku?
A. 16 C. 21
B. 20 D. 32

6. PromieŇĄ okrńôgu wpisanego w tr√≥jkńÖt r√≥wnoboczny o boku 12 cm ma dŇāugoŇõńá: A. 36^cm B. 4\'3cm C. 6V3cm D. 2v/3cm
7. OkrńÖg o Ňõrodku C ma promieŇĄ dŇāugoŇõci 5 cm, a okrńÖg o Ňõrodku B ma promieŇĄ dŇāugoŇõci 3 cm. Podaj dŇāugoŇõńá odcinka BC, jeŇõli okrńôgi sńÖ styczne wewnńôtrznie.
8. Skonstruuj oŇõmiokńÖt foremny wpisany w dany okrńÖg.%
9. Oblicz pole tr√≥jkńÖta ograniczonego prostymi: y = 2x-2 i y = -x + 4 oraz osińÖ x.
10. Wyznacz dŇāugoŇõci bok√≥w narysowanego tr√≥jkńÖta.
C

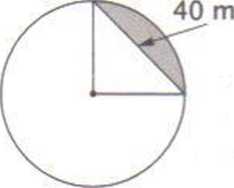
11. Pewien trawnik ma ksztaŇāt czńôŇõci koŇāa, zaznaczonej na rysunku. Ile opakowaŇĄ nawozu do trawy trzeba kupińá, jeŇõli jedno opakowanie wystarczy na 1 ar?
*12. Tr√≥jkńÖt prostokńÖtny ma przyprostokńÖtne dŇāugoŇõci 9 cm i 12 cm. Na tr√≥jkńÖcie opisano i w tr√≥jkńÖt wpisano okrńÖg. Oblicz sumńô dŇāugoŇõci Ňõrednic tych okrńôg√≥w.
Wyszukiwarka
Podobne podstrony:
Matematyka III Sprawziany dla Gimnazjum�32 GRUPA A WIELOKńĄTY, KOŇĀA I OKRńėGI 1. W
Matematyka III Sprawziany dla Gimnazjum�31 WIELOKńĄTY, KOLA I OKRńėGIGRUPA A 1. W kaŇľdym r√≥wnolegŇāob
wielokaty ko?a i okr?gi A GRUPA AWIELOKńĄTY, KOŇĀA I OKRńėGI 1. W kaŇľdym r√≥wnolegŇāobo
Matematyka III Sprawziany dla Gimnazjum�32 GRUPA A WIELOKńĄTY, KOLA I OKRńėCI 1. W
zestaw zada? nr 1 A` GRUPA A1ZESTAW ZADAŇÉ NR 1 W oŇõrodku wczasowym ‚ÄěRelaks‚ÄĚ w Zielonce przebywa 150
zestaw zada? nr 3 A` GRUPA A1ZESTAW ZADAŇÉ NR 3 1- Diagram przedstawia jaki obszar dziaŇāki zajmujńÖ kw
Oznaczenia egzaminu spawacza wg PN-EN 287 lub PN EN ISO 9606n 5. Grupy materiaŇāowe wg. ISO/TR 1 5608
przekszta?cenia geometryczne A` GRUPA A NPRZEKSZTAŇĀCENIA GEOMETRYCZNE 1. Aby otrzymańá czworokńÖt MNO
liczby i wyra?enia algebraiczne A` GRUPA A LICZBY I WYRAŇĽENIA ALGEBRAICZNE 1. Iloczyn V21 ‚ÄĘ 73 jest
figury podobne A` GRUPA A 2/t¬Ī 4 2FIGURY PODOBNE 1. Skala podobieŇĄstwa tr√≥jkńÖta F do tr√≥jkńÖta F wy
Obraz (1301) e) moŇľe byńá wielokrotnie niespŇāacany - za kaŇľdym razem po prostu zamieniony zostanie w
oglńÖdy/Zdarzenia ‚Ė† p√≥Ňļniejsze wielokrotne odtwarzanie tych ‚ÄěnagraŇĄ‚ÄĚ r√≥wnolegle z realizowanńÖ w
wińôcej podobnych podstron