~LWF0031 [Rozdzielczo�� Pulpitu]

R. III. Ogólne zasady ruchu cieczy

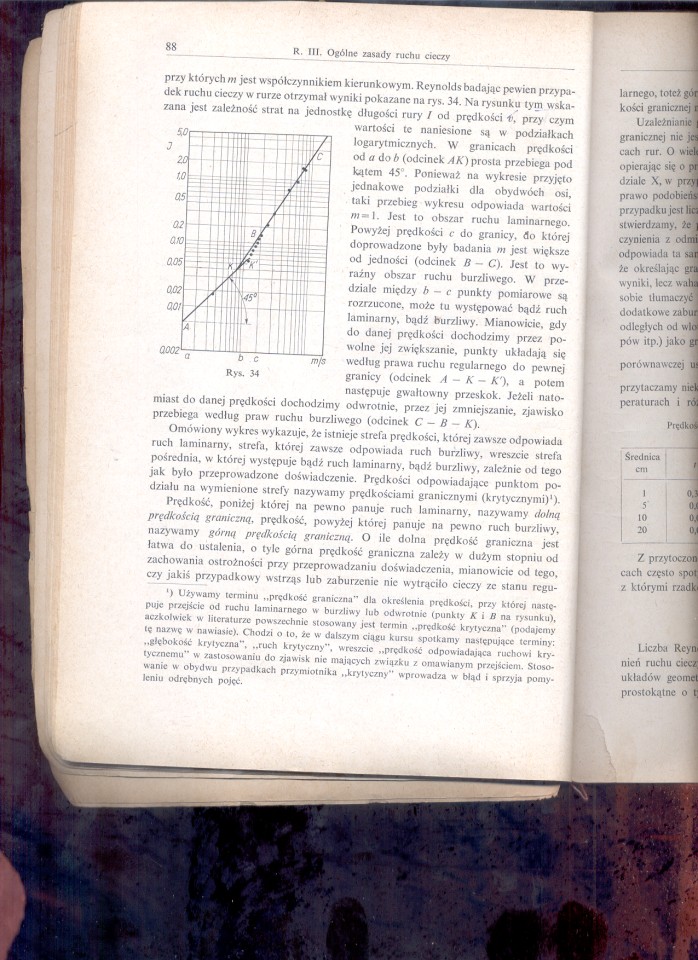
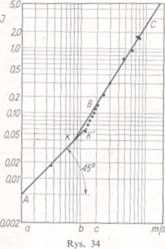
przy których m jest współczynnikiem kierunkowym. Reynolds badając pewien przypadek ruchu cieczy w rurze otrzymał wyniki pokazane na rys. 34. Na rysunku tym wskazana jest zależność strat na jednostkę długości rury / od prędkości i\ przy czym wartości te naniesione są w podziałkach logarytmicznych. W granicach prędkości od a do b (odcinek AK) prosta przebiega pod kątem 45°. Ponieważ na wykresie przyjęto jednakowe podziałki dla obydwóch osi, taki przebieg wykresu odpowiada wartości I. Jest to obszar ruchu laminarncgo. Powyżej prędkości <• do granicy, do której doprowadzone były badania m jest większe od jedności (odcinek B - C). Jest to wyraźny obszar ruchu burzliwego. W przedziale między A-c punkty pomiarowe są rozrzucone, może tu występować bądź ruch laminarny, bądź burzliwy. Mianowicie, gdy do danej prędkości dochodzimy przez, powolne jej zwiększanie, punkty układają się według prawa ruchu regularnego do pewnej granicy (odcinek A - K - A"), a potem następuje gwałtowny przeskok. Jeżeli natomiast do danej prędkości dochodzimy odwrotnie, przez jej zmniejszanie, zjawisko przebiega według praw ruchu burzliwego (odcinek C — B - K).

Omówiony wykres wykazuje, że istnieje strefa prędkości, której zawsze odpowiada ruch laminarny, strefa, której zawsze odpowiada ruch burzliwy, wreszcie strefa pośrednia, w której występuje bądź ruch laminarny, bądź burzliwy, zależnie od tego jak było przeprowadzone doświadczenie. Prędkości odpowiadające punktom podziału na wymienione strefy nazywamy prędkościami granicznymi (krytycznymi)').

Prędkość, poniżej której na pewno panuje ruch laminarny. nazywamy dolną prędkością graniczną, prędkość, powyżej której panuje na pewno ruch burzliwy, nazywamy górną prędkością graniczną. O ile dolna prędkość graniczna jest łatwa do ustalenia, o tyle górna prędkość graniczna zależy w dużym stopniu od zachowania ostrożności przy przeprowadzaniu doświadczenia, mianowicie od tego. czy jakiś przypadkowy wstrząs lub zaburzenie nic wytrąciło cieczy ze stanu regu-') Używamy terminu „prędkość graniczna” dla określenia prędkości, przy której następuje przejście od ruchu laminarncgo w burzliwy lub odwrotnie (punkty A' i B na rysunku), aczkolwiek w literaturze powszechnie stosowany jest termin ..prędkość krytyczna" (podajemy tę nazwę w nawiasie). Chodzi o to. że w dalszym ciągu kursu spotkamy następujące terminy: „głębokość krytyczna", „ruch krytyczny”, wreszcie „prędkość odpowiadająca ruchowi krytycznemu" w zastosowaniu do zjawisk nic mających związku z omawianym przejściem. Stosowanie w obydwu przypadkach przymiotnika „krytyczny" wprowadza w błąd i sprzyja pomyleniu odrębnych pojęć.

łarnego, toteż kości grunii Uzależni: graniczJKj nic j cach rur. 0 opierając się o dziale X, w pi prawo podobieńs przypadku jest lic stwierdzamy, że ; czynienia z odia odpowiada ta sfl że określając gfl wyniki, lecz wafl sobie tłumaczy* dodatkowe zabił odległych od wił pów itp.) jako '

porównawczej 1

przytaczamy nia peraturach i rćj

Liczba Rcyn nień ruchu cieci układów geomd prostokątne o j