FizykaII16701

101

trzeba jeszcze należycie opiłować, póki wirowanie krzywicy, przez naznaczony punkt p w mikroskopie opisanej, całkiem nie-' ustanie. Tym sposobem można wyrabiać diapasony zupełnie jeduozgodne z diapasonem wzorowym,'tudzież diapasony w ogóle z przestankami doskonale czystemu

, \

*

§ 30. 0 tonauT, wywołanych drganiem ciał stałych. Ciała stałe mogą być wprawione w drgania podłużne, poprzeczne i obrotowe czyli wirowe, stosownie do kierunku, w którym się ich sprężystość do objawu pobudź. Każdy z tych trzech rodzajów drgania wydaje tony, gdyż przez nie bywa też otaczające powietrze w drganie wprawione, a to przewodzi je do naszego ucha. Liczba drgań N. pręta, wykonującego podłużne oscylacye, oznacza się (§ 12) wyrażeniem

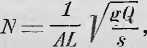
w którym A jego długość, w gęstość, a Q współczynnik elastyczności jego przedstawia. Ton więc podłużny pręta nie zależy wcale od grubości czyli poprzecznego przecięcia jego. Że tak jest w samej rzeczy, stwierdził liczuemi doświadczeniami już Chla-dni, który badał podłużne drgania prętów i ich tony pierwej, nim jeszcze teoryę tych ruchów⁷ rozwinięto. *) Według powyższego wzoru liczba drgań, a z nią także wysokośfl tonu w prętach, drgających podłużnie, powinna w równych zresztą okolicz" nościaeh proporcyonalną być do drugiego’ pierwiastku z ilorazu otrzymanego z podzielenia elastyczności przez gęstość. Chladni udowodnił to na drodze doświadczenia, Wprawiając w⁷ drgania pręty dwie stopy długie na obu końcach wolne i dobywając z nich różne tony, np. z pręta srebrnego 15 próby, ton r/₄, z miedzianego g₄, z żelaznego c«₅.

Liczby drgań tych tonów dla c₄ = 1 mają się do siebie, jak 7b : % : ²⁵/i2, albo dla d_i 1, -jak 1 : ⁴/₃ : ⁵%₇, a kładąc wartość tonów temperowanymi naresżcie. jak 1 : 1-33184 : 1-88775.

*) Chladui, Aku-tlk pag. 103    1C9.

Fizyka T. II.

\