008 bmp

który opisuje błąd średni kwadratowy, wyrażający z większym prawdopodobieństwem

realny graniczny błąd pomiaru w przypadku dużej liczby mierzonych bezpośrednio wielkości.

Jako przykład wyznaczony będzie maksymalny błąd systematyczny pomiaru rezystancji R metodą pośrednią na podstawie pomiaru napięcia U i prądu 1 (rys. 1.2).

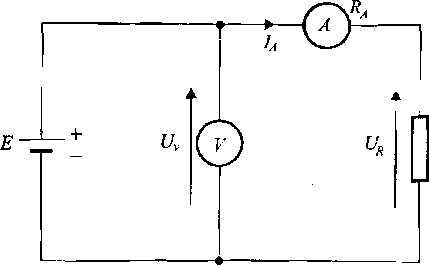
Rys. 1.2. Układ do pośredniego pomiaru rezystancji R_x

Pomiary bezpośrednie wykonywane woltomierzem i amperomierzem obarczone są błędami maksymalnymi AU i Al, które związane są z dokładnością zastosowanych mierników' i mogą być wyznaczone na podstawie znajomości ich klas dokładności (rozdział 2).

Wartość rezystancji wyznaczona w układzie jak na rysunku 1.2 ze stosunku wskazań woltomierza i amperomierza

(M9)

różni się od rzeczywistej wartości rezystancji R_x wyznaczonej ze stosunku napięcia U_R panującego na oporniku i prądu I_A płynącego przez opornik

_R_U'_U_r-I_tR_A "'"Z." I. ~^R‘

R.

(1.20)

gdzie R_a - rezystancja weumętrzna amperomierza.

Błąd systematyczny metody należy uwzględnić w^r formie poprawki ze znakiem ujemnym o wartości równej rezystancji wewmętrznej amperomierza.

Błąd systematyczny wynikający z prawa sumowania się błędów' (1.17) obliczony z zależności R = Ujl ma postać

AR =

AU

h

(1.21)

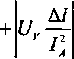
Wynik pomiaru rezystancji opornika metodą przedstawioną na rysunku 1.2 uwzględniający błędy systematyczne wynosi

(1.22)

R = R_;m -R_a±AR

1.4. Wyznaczanie błędów przypadkowych

Analizę błędów przypadkowych przeprowadza się przy wykorzystaniu statystyki matematycznej, przyjmując założenie potwierdzone praktycznie, że rozkład błędów przypadkowych traktowanych jako zmienna losowa odpowiada rozkładowi normalnemu. Założenie to nie zawsze jest ściśle spełnione, gdyż nieuchwytne ilościowo wpływy systematyczne osłabiają przypadkowość, skutkiem czego powstają odchylenia od rozkładu normalnego zależnie od kierunku i natężenia tych wpływów. Jeżeli liczba pomiarów nie jest odpowiednio duża, trudno również dokładnie ocenić parametry rozkładu błędów przypadkowych. W tych przypadkach dąży się do zastąpienia danego rozkładu zastępczym rozkładem normalnym i oceny dokładności otrzymanego przybliżenia.

Rozkład błędów przypadkowych zgodny z rozkładem normalnym charakteryzuje funkcja prawdopodobieństwa

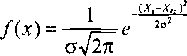
(1.23)

gdzie: Xi - wynik i-tego pomiaru,

a - odchylenie standardowe.

Wykres funkcji^) - krzywa Gaussa - przedstawiony jest na rysunku 1.3

m

'V(A)

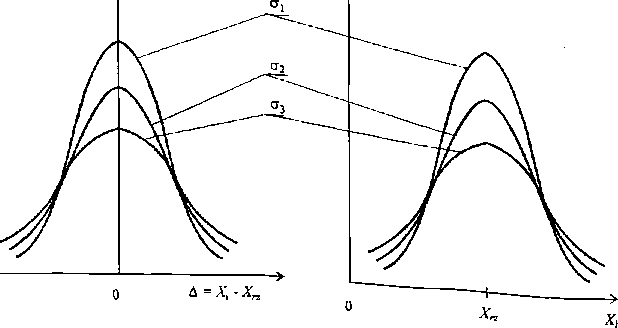
^Rys. 1.3, Wykres funkcji gęstości prawdopodobieństw;

>w przypadkowych

^{a r}°^Zkladu normalnego błędem

17