0163

165

§ 2. Fole i objętość

Przede wszystkim łatwo jest udowodnić, że własność tę ma każda krzywa ciągła, która ma równanie nieuwikłane postaci

(5)    y=.f(x) (a^x^b) lub x = g(y) (c<y<d),

gdzie fig są funkcjami ciągłymi.

Przypuśćmy na przykład, że mamy do czynienia z pierwszym z tych równań. Przy

danym e > 0 przedział <a, ó> można podzielić na takie podprzedziały <x₍,x₍+₁> (i =

= 0,1, ... , n—1), żeby w każdym z nich oscylacja funkcji/była mniejsza od    [87].

o—a

Jeśli oznaczymy, jak zwykle, przez m_t i M_t wartość najmniejszą i największą funkcji / w i-tym przedziale, to figura złożona z prostokątów

<*i, *1+1 ; wi„ M,y (i = 0,1,..., n -1)

pokryje całą naszą krzywą (patrz rys. 17), przy czym pole tej figury będzie równe

Y (Af,-m,) (x_ł+1 -x₍) =    ^Axi

b—a

Y^*i =

co należało właśnie udowodnić. Krzywa (5) ma więc pole równe 0. Wynika stąd, co następuje:

Jeśli figura P jest ograniczona kilkoma krzywymi ciągłymi, z których każda z osobna ma równanie postaci (5) (Jednego lub drugiego typu), to figura ta jest mierzalna.

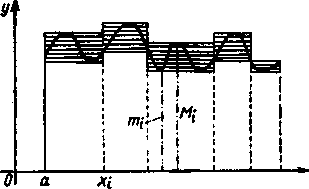
Xi+1

Rys. 17

Rzeczywiście, ponieważ każda z wymienionych krzywych ma pole równe 0, więc oczywiście również cały kontur ma pole równe 0.

Z tego kryterium można otrzymać inne, mniej ogólne, które jednakże w praktyce okazuje się wygodniejsze.

Krzywą daną równaniami parametrycznymi (6) x = g>(t), y-v(t) (t₀ < t < T) , nazywamy gładką, jeśli 1) funkcje ę i yi mają ciągłe pochodne w całym przedziale <r₀, T> zmienności parametru i 2) krzywa nie ma punktów wielokrotnych, ani w ogóle punktów osobliwych. W przypadku krzywej zamkniętej żądamy jeszcze, żeby spełnione były równości

<p'0o) = <P'(T),    _V'(t₀) = _V'(T).

Pokażemy teraz, że każda krzywa gładka ma pole równe 0.

Niech M* oznacza dowolny punkt na krzywej, określony przez wartość t* parametru. Ponieważ nie jest to punkt osobliwy, więc —jak widzieliśmy [223] — istnieje taki przedział:

O* =    <*+a*>,

że odpowiadający mu łuk krzywej można przedstawić równaniem postaci (5).