0195

197

§ 3. Obliczanie wielkości mechanicznych i fizycznych

W szczególności dla półkola d = 2r, s = nr i

t) = — r ** 0,637 r.

TC

4)    Znaleźć środek ciężkości luku cykloidy

x = a (/—sin t), y — a (1—cos t) (0 < t < 27t).

Biorąc pod uwagę symetrię od razu widać, że £ = ita. Po uwzględnieniu wyniku przykładu 4) z ustępu 345, łatwo otrzymujemy ij = Ą- a.

5)    W tych przypadkach, kiedy z góry znane jest położenie środka ciężkości, można użyć twierdzenia Guldina do wyznaczania pola powierzchni obrotowej.

Przypuśćmy na przykład, że należy wyznaczyć pole powierzchni torusa (pierścienia), tzn. bryły powstającej przez obrót koła dokoła nieprzecinającej go osi (rys. 40). Ponieważ oczywiste jest, że środek ciężkości koła pokrywa się z jego środkiem geometrycznym, więc, przy oznaczeniach podanych na rysunku, mamy

|P| = 2nr • 2nd — 4n² rd.

351. Wyznaczanie momentów statycznych i środka ciężkości figury płaskiej. Rozpatrzymy figurę płaską AA 'B'B (rys. 41), ograniczoną od góry krzywą AB, która dana jest równaniem y — f(x). Załóżmy, że masa jest rozłożona na tej figurze równomiernie, tak że gęstość powierzchniowa q (tj. masa przypadająca na

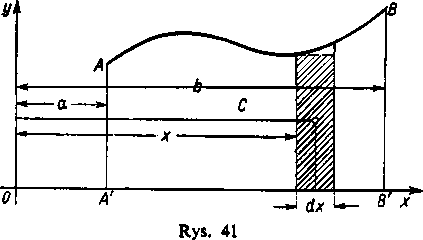
jednostkę pola) jest stała. Bez istotnego zmniejszenia ogólności można wtedy przyjąć, że e = 1, czyli że masa dowolnej części naszej figury jest równa polu tej części. To mamy też zawsze na myśli, jeśli mówimy po prostu o momentach statycznych lub o środku ciężkości figury płaskiej bez zaznaczania, jak jest rozłożona masa.

Chcąc obliczyć momenty statyczne Af„ i Af, tej figury względem osi współrzędnych wydzielimy, jak zwykle, dowolny element naszej figury w postaci nieskończenie wąskiego paska (patrz rysunek). Przyjmując w przybliżeniu, że pasek ten jest prostokątem, widzimy, że jego masa (wyraźąjąca się tą samą liczbą, co i pole) jest równa y dx. Aby wyznaczyć odpowiednie momenty elementarne dM_x i dM,, zakładamy, że cała masa paska jest skoncentrowana w jego środku ciężkości (tzn. w środku prostokąta), co, jak wiadomo, nie zmienia wielkości momentów statycznych. Otrzymany punkt materialny leży w odległości (x+ -i- dx) od osi y\ ostatnie wyrażenie można zastąpić po prostu przez x, ponieważ odrzucony składnik -i- dx pomnożony przez masę y dx daje nieskończenie małą wyższego rzędu. Mamy zatem

dM_x = -jy¹ dx, dM, = xydx .

Sumując te momenty elementarne otrzymujemy wynik

»    b

(»)    M_x = J jy¹ dx , M, = f xydx,

a    i

przy czym przez y rozumiemy funkcję f(x) z równania krzywej AB.