0193

195

§ 3. Obliczanie wielkości mechanicznych i fizycznych

gdzie m,, m₂, ..., m„ oznaczają masy tych punktów. Przy tym odległości od osi punktów leżących po jednej stronie tej osi przyjmujemy za dodatnie, a odległości punktów leżących po drugiej stronie — za ujemne.

Jeśli masa nie jest skoncentrowana w oddzielnych punktach, ale jest rozłożona w sposób ciągły, wypełniając krzywą lub figurę płaską, to do wyrażenia momentu statycznego potrzebujemy nie sumy, lecz całki.

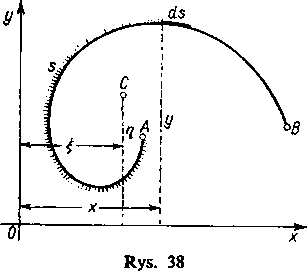
Zatrzymamy się na określeniu momentu statycznego M względem osi x masy rozłożonej wzdłuż pewnej krzywej płaskiej AB (rys. 38). Załóżmy przy tym, że krzywa jest jednorodna, tzn., że jej gęstość liniowa p (czyli masa przypadająca na jednostkę długości) jest stała; dla uproszczenia przyjmiemy, że jest nawet p = 1 (w przeciwnym przypadku wystarczy pomnożyć wynik przez p). Przy tych założeniach masa dowolnego łuku naszej krzywej jest równa po prostu jego długości i pojęcie momentu statycznego nabiera charakteru czysto geometrycznego. Zauważmy ogólnie, że jeśli będziemy mówili o momencie statycznym (lub o środku ciężkości) krzywej bez omówienia rozkładu masy wzdłuż tej krzywej, to zawsze będziemy mieli na myśli moment statyczny (lub środek ciężkości) określony właśnie przy podanych założeniach.

Rozpatrzmy teraz jakikolwiek element łuku ds krzywe]

(którego masa również wyraża się liczbą ds). Jeśli przyjmiemy ten element w przybliżeniu za punkt materialny, leżący w odległości y od osi, to moment statyczny tego elementu jest równy

dM_x = y ds.

Sumując takie częściowe momenty statyczne i biorąc przy tym za zmienną niezależną długość łuku s, otrzymamy następujące wyrażenie na moment statyczny:

(4)

M_x = j yds . 0

Analogicznym wzorem wyraża się moment statyczny względem osi y

s

(5)    M_y = J x ds.

o

Oczywiście zakłada się tu, że y (lub z) wyraża się przez s. W praktyce we wzorach tych wyraża się s przez tę zmienną (r, x lub 6), która gra rolę zmiennej niezależnej w analitycznym przedstawieniu krzywej.

Znając momenty statyczne M_x i M, krzywej łatwo można znaleźć położenie jej środka ciężkości C (f, ł>). Punkt C ma tę własność, że jeśli skoncentrować w nim całą „masę” krzywej (równą jej długości), to moment tego punktu względem dowolnej osi jest taki sam, jak moment krzywej względem tej osi. Jeśli weźmiemy w szczególności momenty krzywej względem osi układu współrzędnych, to znajdziemy

S

51 — M_y — J x ds, o

s

Si] = M_x = f yds, o

skąd

(6)

S    5

O    O

Ze wzoru na rzędną t\ środka ciężkości otrzymujemy interesujący wniosek geometryczny. Mamy bowiem

s    s

rjS = J y ds, skąd 2icrjs = 2iz J y ds ; o    o

13*