0201

203

§ 3. Obliczanie wielkości mechanicznych i fizycznych

pierścienie koncentryczne, tak że ciśnienie P rozkłada się na ciśnienia elementarne odpowiadąjące poszczę* gólnym pierścieniom. Rozpatrujemy teraz pierścień ograniczony kołami o promieniach r i r+dr (na rys. 45b) pierścień ten jest zakreskowany). Pole tego pierścienia wynosi

n {r+dr)¹—nr² = 2nr dr+n (dr)¹;

odrzucając nieskończenie małą n (dr)² rzędu drugiego, możemy przyjąć, że pole to jest w przybliżeniu rów* ne liardr. Jeśli p oznacza ciśnienie (na jednostkę pola) w punkcie odległym od środka o r, to rozpatrywanemu pierścieniowi odpowiada ciśnienie elementarne

dP = p • 2Ttr dr,

skąd przez sumowanie i przejście do granicy otrzymujemy równość

R

(11)    P = 2k jpr dr.

'o

Powtarzamy, że równość ta wyraża fakt, iż całkowite ciśnienie rozłożone na czopie jest równe ciśnieniu wału.

Wyznaczymy teraz moment M względem osi obrotu siły tarcia dla obracającego się czopa. Rozpatrzymy ponownie pierścień elementarny, o którym była mowa wyżej; siła tarcia pochodząca od tego pierścienia przeciwdziała obrotowi i jest równa

pdP = 2n ftpr dr,

tak że odpowiadający jej moment elementarny dM wyraża się iloczynem tej siły przez ramię r (wspólne dla wszystkich punktów pierścienia)

dM = 2jt ppr² dr

wobec tego moment siły tarcia wynosi

R

(12)    M — tnp J pr² dr.

'o

Jak wiadomo z mechaniki praca A wykonana przez taki stały moment obrotowy M w czasie 1 sek jest równa iloczynowi momentu M przez prędkość kątową obrotu co (1/sek)

A - Mm.

Aby doprowadzić do końca obliczenie pracy A, należy teraz uczynić jakieś założenia o funkcji roz. kładu ciśnienia p na powierzchni czopa.

Najprostsze jest założenie, że rozkład ciśnienia jest równomierny, tzn. że p = const. Wielkość tej stałej wyznacza się z warunku (11). Wobec tego jest bezpośrednio widoczne, że jeśli ciśnienie rozkłada się równomiernie po polu n (R²—r%) pierścienia, to na jednostkę pola przypada ciśnienie

P = c =

P

rc(R²-rg)!*

Podstawiając tę wartość zamiast p we wzorze (12), znajdujemy następnie

P

*(R²-r²0)

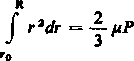
R³-rl R²-r% '

M = lup.

W szczególności dla pełnego czopa jest M — y fiPR.

Wyniki te można jednak stosować tylko do czopów nowych, jeszcze nie dotartych. Rzecz w tym, że przy obrocie wału punkty czopa bardziej oddalone od środka O poruszają się z większą prędkością liniową, w punktach tych praca tarcia jest większa i wobec tego większe jest zużycie zarówno czopa, jak i łożyska. Dzięki temu część ciśnienia przenosi się na części czopa bliższe środka. Dla czopów starych wysłu-