019

2 GEOMETRICKE ZNAZORNENI KOMPLEXNICH ĆISEL

Ncmo nascitur sapiens. Nikdo se nerodi rnoudrym.

2.1 Komplexm ćisla jako body Gaussovy roviny

Na zaćatku uvodni kapitoly jsme si pripomenuli, że existuje vza-jemne jednoznaćne zobrazeni mezi mnożinou R a mnożinou vsech bodu primky; existence tohoto zobrazeni umożnuje na zvolenć primce realna ćisla znazornit. Existuje vsak i vzajemne jednoznaćne zobrazeni mezi mnożinou RxR vsech usporadanych dvojic realnych ćisel a mnożinou v§ech bodu dane roviny; vyuźivame toho vżdy, kdyź v rovine volime souradnicovou soustavu. Uvedorm'me-li si, że usporadanym dvojicim realnych ćisel mużeme priradit ćisla komplexni, je zrejme, że kom-plexni ćisla mużeme znazornit jako body roviny. Tuto rovinu buderne nazyvat rovinou komplexnich ćisel nebo ćasteji Gaussovou rovinou.

Rovina komplexnich ćisel neboli Gaussova rovina je rovina, jejiż body povażujeme za obrazy komplexnich ćisel.

Vzajemne prirazeni komplexnich ćisel a bodu Gaussovy roviny je zprostredkovano pomoci kartezske souradnicove soustavy Oxy, na jejiż oso x jsou zobrazena ćisla realna (tj. komplexni ćisla tvaru a + Oi) a na ose y ćisla ryzę imaginarni (tj. komplexni ćisla tvaru 0 + 6i); osa x se nazyva realna osa, osa y imaginarni osa. Abychom se mohli vyjadrovat jednoduśe. buderne nekdy misto o obrazu komplexniho ćisla mluvit primo o ćisle z. Na obrazcich budou proto body zobrazujici ćisla oznaćeny primo ćisly, ktera zobrazuji; napr. na obr.2.1 jsou pro ilustraci kromę ćisel znazornenych na realne a imaginarni ose zobrazena komplexni ćisla 3 + 3i, 3 — 3i, —3 — 3i, —2 + i, —2 — i. Je zrejme, że obrazy ćisel sdrużenych jsou soumerne podle realne osy a obrazy ćisel opaćnych jsou soumerne podle poćatku.

Obr. 2.1

Yratme se ke zndzomeni realnych ćisel na ćiselne ose a pripo-meńme si, że absolutni hodnota libovolneho realneho ćisla je rovna vzdalenosti jeho obrazu od poćatku na ćiselne ose. Ma tuto vlastnost i absolutni hodnota ćisel komplexnich?

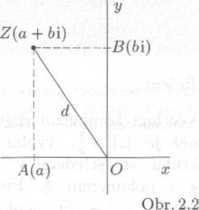
Zkoumejme proto vzdalenost d bodu Z, ktery je obrazem komplex-niho ćisla z = a + bi, od poćatku O (viz obr. 2.2, kde bod A je obrazem realneho ćisla a, bod B obrazem ryzę imaginarniho ćisla bi).

Plati:

d - \OZ\ = V\OA]² + \OB\². Yzhledem k tomu, że

\OA\ — |o.|,    | OB\ = \b\,

dostavame

-3

-2 +i r—

—2' -1

i—

-2-i

i----

-3 — 3i

3 + 3i ---T

O 1    2

—i

—2i -3i~

----i

3 — 3i

d = \/|a|² + |6|² = \Ja'² + b².