034

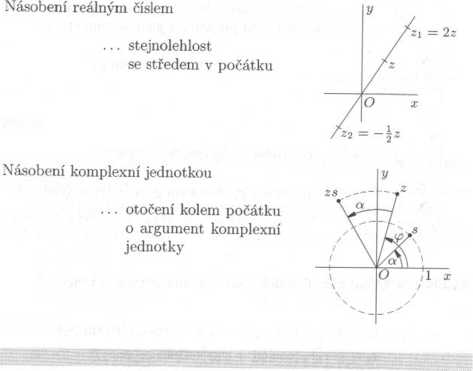
Graficke sćitani a nasobeni komplexnich ćisel

Sćitani

... sćitani vektoru

	y	Z\+ z
	/ y	^r\
Z2 '		\ \
		Jz 1
	o	X

ULOHY K OPAKOVANI

2.26 Zobrazte v Gaussove rovine nmożinu vsech komplexnfch ćisel z. pro neź plati:

a) \z\ = |z + 2i|    b) \z - l| = \z + i| = \z\

^c) 1| = N ~ i|    cl) |z-l|<|z + i|

2.27 Zapiśte v goniometrickem tvaru cisi a:

a) cos² + i sin²

b) 5\/3 + 5i

c)

1 +i 1 - i

d)

1 -i 1 + i

(1 + i)²⁰

b)

d)

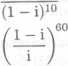
2.28 Vypoct.ete: a) (V3 + i)²°

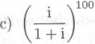
2.29 Ukaźtc użitim Moivreovy vety, że plati:

a)    sin(a + 3) = cos a sin 3 + sin a cos 13

b)    cos (a + 3) = cos a cos i3 - sin o sin 3

2.30 Użitim Moivreovy vety vyjadrete sin5x, cos 5x pomoci mocnin sinx, cos x.

2.31    Vypoćtete:

a)    (sin fu+ i cos fuj

b)    (tg 1 — i)⁴

c)    (cos o + isina)ⁿ + (cos a + i sina)^-”, n e N

V6+V2    V6-s/2 .

2.32 Vite-li, że komplexni jednotka s = -— --1--- i ma

argument = yjit, urccte v algebraickem i v goniometrickem tvaru komplexni jednotku s argumentem:

a)    b) jfit    c)    d)

*2.33 Zapiśte v goniometrickem tvaru cisla:

a)

cos a + i sin a

cos 3 + i sin 3 c) (coso - i sina)⁷¹, n € N

cos a + i sin a cos 3 ~ i sin 3 1 + i tg a'

1 - i tg a

n € N

67